LitCTF2023

AK赛

这里只有密码的wp

rank:2

Hex？Hex！

直接十六进制转字符串

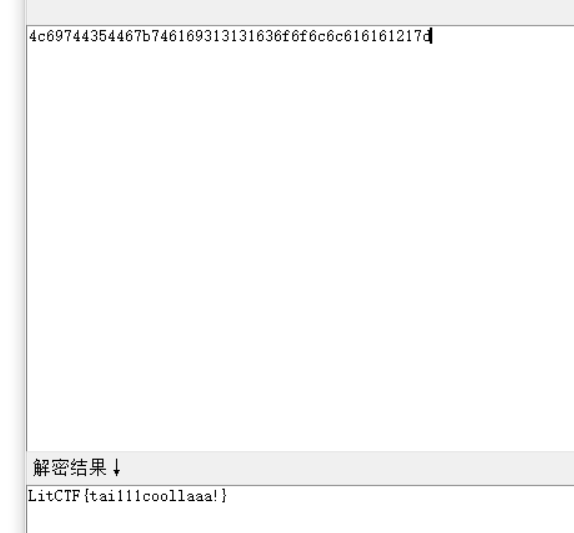
LitCTF{tai111coollaaa!}

梦想是红色的

核心价值观编码

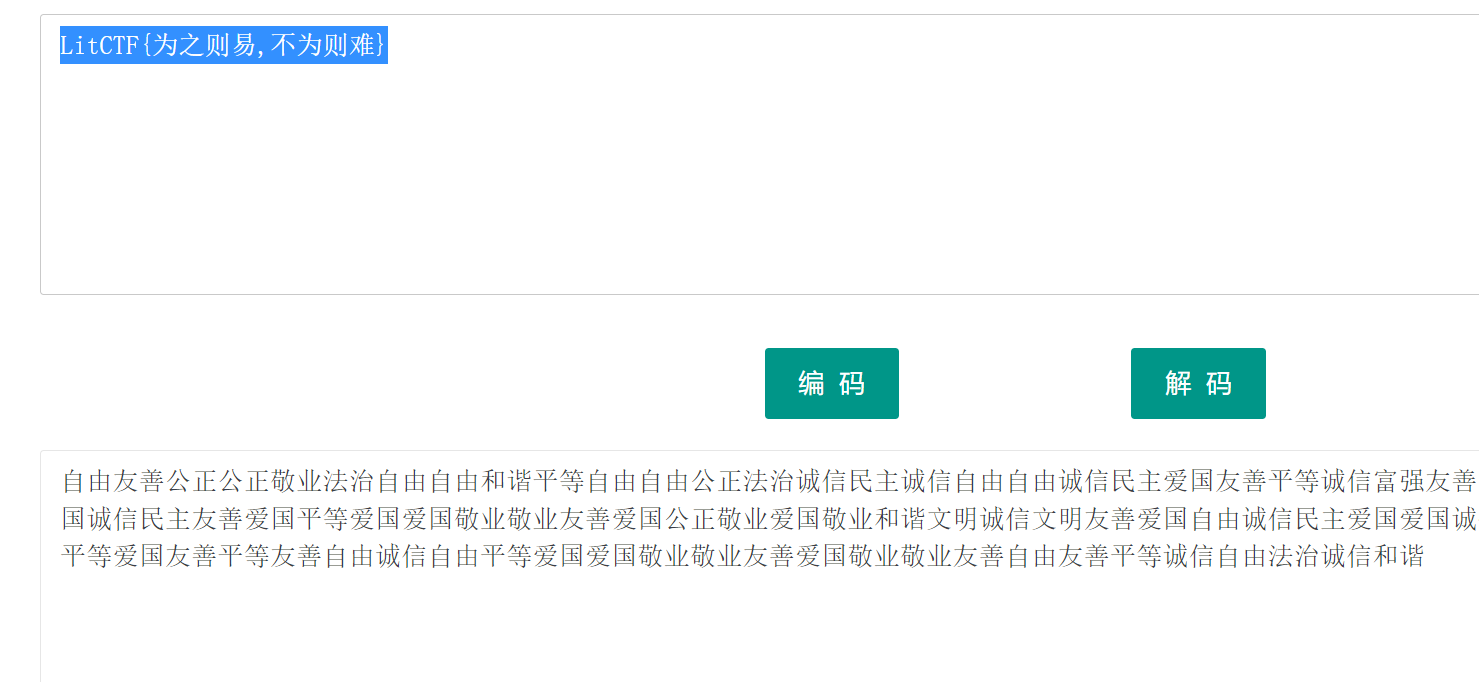
LitCTF{为之则易,不为则难}

factordb

直接分解n求RSA

import libnum
import gmpy2

e = 65537
n = 87924348264132406875276140514499937145050893665602592992418171647042491658461
c = 87677652386897749300638591365341016390128692783949277305987828177045932576708
p=319576316814478949870590164193048041239
q=275127860351348928173285174381581152299
phi=(p-1)*(q-1)
d=gmpy2.invert(e,phi)
m=pow(c,d,n)
print(libnum.n2s(int(m)))
# LitCTF{factordb!!!}

家人们！谁懂啊，RSA签到都不会

简单RSA

import libnum
import gmpy2

e = 65537
p = 12567387145159119014524309071236701639759988903138784984758783651292440613056150667165602473478042486784826835732833001151645545259394365039352263846276073
q = 12716692565364681652614824033831497167911028027478195947187437474380470205859949692107216740030921664273595734808349540612759651241456765149114895216695451
c = 108691165922055382844520116328228845767222921196922506468663428855093343772017986225285637996980678749662049989519029385165514816621011058462841314243727826941569954125384522233795629521155389745713798246071907492365062512521474965012924607857440577856404307124237116387085337087671914959900909379028727767057
n=p*q
phi=(p-1)*(q-1)
d=gmpy2.invert(e,phi)
m=pow(c,d,n)
print(libnum.n2s(int(m)))
# LitCTF{it_is_easy_to_solve_question_when_you_know_p_and_q}

yafu

可以直接用sage euler_phi(n)来求phi

sage

import libnum
import gmpy2
n = 15241208217768849887180010139590210767831431018204645415681695749294131435566140166245881287131522331092026252879324931622292179726764214435307
c = 12608550100856399369399391849907846147170257754920996952259023159548789970041433744454761458030776176806265496305629236559551086998780836655717

e = 65537
phi=euler_phi(n)
d=gmpy2.invert(e,phi)
m=pow(c,d,n)
print(libnum.n2s(int(m)))
# LitCTF{Mu1tiple_3m4ll_prim5_fac7ors_@re_uns4f5}

P_Leak

dp泄露直接套脚本

import libnum
import gmpy2
e=65537
dp= 5892502924236878675675338970704766304539618343869489297045857272605067962848952532606770917225218534430490745895652561015493032055636004130931491316020329
n= 50612159190225619689404794427464916374543237300894011803225784470008992781409447214236779975896311093686413491163221778479739252804271270231391599602217675895446538524670610623369953168412236472302812808639218392319634397138871387898452935081756580084070333246950840091192420542761507705395568904875746222477
c= 39257649468514605476432946851710016346016992413796229928386230062780829495844059368939749930876895443279723032641876662714088329296631207594999580050131450251288839714711436117326769029649419789323982613380617840218087161435260837263996287628129307328857086987521821533565738409794866606381789730458247531619


for i in range(1,65535):
    p=(dp*e-1)//i+1
    if n%p==0:
        q=n//p
        break
print(p)
print(q)
phi_n= (p-1)*(q-1)
d=gmpy2.invert(e,phi_n)
m=pow(c,d,n)
print(m)
flag=libnum.n2s(int(m)).decode()
print(flag)
# LitCTF{Prim3_1s_Le@k!!!!!}

easy_math

直接解方程

n = 2230791374046346835775433548641067593691369485828070649075162141394476183565187654365131822111419512477883295758461313983481545182887415447403634720326639070667688614534290859200753589300443797
c = 2168563038335029902089976057856861885635845445863841607485310134441400500612435296818745930370268060353437465666224400129105788787423156958336380480503762222278722770240792709450637433509537280
hint = 392490868359411675557103683163021977774935163924606169241731307258226973701652855448542714274348304997416149742779376023311152228735117186027560227613656229190807480010615064372521942836446425717660375242197759811804760170129768647414717571386950790115746414735411766002368288743086845078803312201707960465419405926186622999423245762570917629351110970429987377475979058821154568001902541710817731089463915930932142007312230897818177067675996751110894377356758932


import libnum
import gmpy2
import sympy

p=sympy.Symbol('p')
q=sympy.Symbol('q')
f1=p*q-n
f2=p**3-q**5 -hint
result=sympy.solve([f1,f2],[p,q])
print(result)
e=65537
p=7321664971326604351487965655099805117568571010588695608389113791312918573783115429227542573780838065461696504325762281209452761930184231131129306271846427
q=304683618109085947723284393392507415311
phi=(p-1)*(q-1)
d=gmpy2.invert(e,phi)
m=pow(c,d,n)
print(libnum.n2s(int(m)))
#LitCTF{f9fab7522253e44b48824e914d0801ba}

e的学问

e和phi不互素直接套脚本

e=74
p= 86053582917386343422567174764040471033234388106968488834872953625339458483149
q= 72031998384560188060716696553519973198388628004850270102102972862328770104493
c= 3939634105073614197573473825268995321781553470182462454724181094897309933627076266632153551522332244941496491385911139566998817961371516587764621395810123
import gmpy2
from Crypto.Util.number import *


# 当e约去公约数后与phi互素
def decrypt(p, q, e, c):
    n = p * q
    phi = (p - 1) * (q - 1)
    t = gmpy2.gcd(e, phi)
    d = gmpy2.invert(e // t, phi)
    m = pow(c, d, n)
    print(m)
    msg = gmpy2.iroot(m, t)
    print(msg)
    if msg[1]:
        print(long_to_bytes(msg[0]))
decrypt(p, q, e, c)
#LitCTF{e_1s_n0t_@_Prime}

原来你也玩原神

对照即可

{yuanlainiyewanyuanshenwww}

转化为大写

NSSCTF{YUANLAINIYEWANYUANSHENWWW}

你是我的关键词(Keyworld)

根据题目名称直接手撸

IFRURC{X0S_YP3_JX_HBXV0PA}
LITCTF{Y0U_AR3_MY_KEYW0RD}

Is this only base?

SWZxWl=F=DQef0hlEiSUIVh9ESCcMFS9NF2NXFzM

栅栏23栏

SWZxWlFDe0liUV9ScF9FNFMzX2NSMCEhISEhfQ==

base64

IfqZQC{IbQ_Rp_E4S3_cR0!!!!!}

凯撒

LitCTF{LeT_Us_H4V3_fU0!!!!!}

md5的破解

直接上脚本了

import string
from hashlib import md5
c=string.digits+string.ascii_lowercase
for i in c:
    for j in c:
        for o in c:
            for p in c:
                flag='LitCTF{md5can'+i+j+'3de'+o+'rypt213thoughcr'+p+'sh}'
                if  md5(flag.encode()).hexdigest() == '496603d6953a15846cd7cc476f146771':
                    print(flag)
                    break
#LitCTF{md5can123dexrypt213thoughcrpsh}

The same common divisor

利用公因数求p，然后RSA

import libnum
import gmpy2
e=65537
n1= 9852079772293301283705208653824307027320071498525390578148444258198605733768947108049676831872672654449631852459503049139275329796717506126689710613873813880735666507857022786447784753088176997374711523987152412069255685005264853118880922539048290400078105858759506186417678959028622484823376958194324034590514104266608644398160457382895380141070373685334979803658172378382884352616985632157233900719194944197689860219335238499593658894630966428723660931647038577670614850305719449893199713589368780231046895222526070730152875112477675102652862254926169713030701937231206405968412044029177246460558028793385980934233
n3= 4940268030889181135441311597961813780480775970170156650560367030148383674257975796516865571557828263935532335958510269356443566533284856608454193676600884849913964971291145182724888816164723930966472329604608512023988191536173112847915884014445539739070437180314205284883149421228744714989392788108329929896637182055266508625177260492776962915873036873839946591259443753924970795669864031580632650140641456386202636466624658715315856453572441182758855085077441336516178544978457053552156714181607801760605521338788424464551796638531143900048375037218585999440622490119344971822707261432953755569507740550277088437182
c1= 7066425618980522033304943700150361912772559890076173881522840300333719222157667104461410726444725540513601550570478331917063911791020088865705346188662290524599499769112250751103647749860198318955619903728724860941709527724500004142950768744200491448875522031555564384426372047270359602780292587644737898593450148108629904854675417943165292922990980758572264063039172969633878015560735737699147707712154627358077477591293746136250207139049702201052305840453700782016480965369600667516646007546442708862429431724013679189842300429421340122052682391471347471758814138218632022564279296594279507382548264409296929401260
c2= 854668035897095127498890630660344701894030345838998465420605524714323454298819946231147930930739944351187708040037822108105697983018529921300277486094149269105712677374751164879455815185393395371001495146490416978221501351569800028842842393448555836910486037183218754013655794027528039329299851644787006463456162952383099752894635657833907958930587328480492546831654755627949756658554724024525108575961076341962292900510328611128404001877137799465932130220386963518903892403159969133882215092783063943679288192557384595152566356483424061922742307738886179947575613661171671781544283180451958232826666741028590085269
n2=n3^n1
p=gmpy2.gcd(n1,n2)
q1=n1//p
phi=(p-1)*(q1-1)
d=gmpy2.invert(e,phi)
m=pow(c1,d,n1)
print(libnum.n2s(int(m)))
# LitCTF{TH3_Tw0_nUmb3rs_H@v3_The_sAme_D1v1s0r!!}

Where is P?

首先低指加密求出P

n= 24479907029118467064460793139240403258697681144532146836881997837526487637306591893357774423547391867013441147680031968367449693796015901951120514250935018725570026327610524687128709707340727799633444550317834481416507364804274266363478822257132586592232042108076935945436358397787891169163821061005102693505011197453089873909085170776511350713452580692963748763166981047023704528272230392479728897831538235554137129584665886878574314566549330671483636900134584707867654841021494106881794644469229030140144595938886437242375435914268001721437309283611088568191856208951867342004280893021653793820874747638264412653721
a= 22184346235325197613876257964606959796734210361241668065837491428527234174610482874427139453643569493268653377061231169173874401139203757698022691973395609028489121048788465356158531144787135876251872262389742175830840373281181905217510352227396545981674450409488394636498629147806808635157820030290630290808150235068140864601098322473572121965126109735529553247807211711005936042322910065304489093415276688746634951081501428768318098925390576594162098506572668709475140964400043947851427774550253257759990959997691631511262768785787474750441024242552456956598974533625095249106992723798354594261566983135394923063605
e=3
def de(c, e, n):
    k = 0
    while True:
        mm = c + n*k
        result, flag = gmpy2.iroot(mm, e)
        if True == flag:
            return result
        k += 1
P=de(a,e,n)
66302204855869216148926460265779698576660998574555407124043768605865908069722142097621926304390549253688814246272903647124801382742681337653915017783954290069842646020090511605930590064443141710086879668946

然后就是p得高位攻击

import libnum
import gmpy2
n=24479907029118467064460793139240403258697681144532146836881997837526487637306591893357774423547391867013441147680031968367449693796015901951120514250935018725570026327610524687128709707340727799633444550317834481416507364804274266363478822257132586592232042108076935945436358397787891169163821061005102693505011197453089873909085170776511350713452580692963748763166981047023704528272230392479728897831538235554137129584665886878574314566549330671483636900134584707867654841021494106881794644469229030140144595938886437242375435914268001721437309283611088568191856208951867342004280893021653793820874747638264412653721
p_fake=66302204855869216148926460265779698576660998574555407124043768605865908069722142097621926304390549253688814246272903647124801382742681337653915017783954290069842646020090511605930590064443141710086879668946<<340
e=65537
c= 6566517934961780069851397787369134601399136324586682773286046135297104713708615112015588908759927424841719937322574766875308296258325687730658550956691921018605724308665345526807393669538103819281108643141723589363068859617542807984954436567078438099854340705208503317269397632214274507740533638883597409138972287275965697689862321166613821995226000320597560745749780942467497435742492468670016480112957715214640939272457886646483560443432985954141177463448896521810457886108311082101521263110578485768091003174683555938678346359150123350656418123918738868598042533211541966786594006129134087145798672161268647536724

pbits = p_fake.nbits()
kbits = 340 #p失去的低位
pbar = p_fake & (2^pbits-2^kbits)
print ("upper %d bits (of %d bits) is given" % (pbits-kbits, pbits))
 
PR.<x> = PolynomialRing(Zmod(n))
f = x + pbar
x0 = f.small_roots(X=2^kbits, beta=0.4)[0]  # find root < 2^kbits with factor >= n^0.3
p=x0 + pbar
q=int(n)//int(p)

phi=(p-1)*(q-1)
d=gmpy2.invert(e,int(phi))
m=pow(c,d,n)
print(libnum.n2s(int(m)))
# LitCTF{Y0U_hAV3_g0T_Th3_r1ghT_AnsW3r}

我测你vva

直接写脚本逆回去

cipher='HYEQJvPZ~X@+Bp'
flag=''
for i in cipher:
    x=cipher.index(i)
    if x%2==0:
        flag += chr(ord(i)-x)
    elif x%2!=0:
        flag += chr(ord(i)+x)
print(flag)
# HZCTF{Java666}

Virginia

维吉尼亚解码得

There are moments in life when you miss someone so much that you just want to pick them from your dreams and hug them for real! Dream what you want to dream;go where you want to go;be what you want to be,because you have only one life and one chance to do all the things you want to do.May you have enough happiness to make you sweet,enough trials to make you strong,enough sorrow to keep you human,enough hope to make you happy? Always put yourself in others’shoes.If you feel that it hurts you,it probably hurts the other person, too.The happiest of people don’t necessarily have the best of everything;they just make the most of everything that comes along their way.Happiness lies for those who cry,those who hurt, those who have searched,and those who have tried,for only they can appreciate the importance of people,who have touched their lives.Love begins with a smile,grows with a kiss and ends with a tear.The brightest future will always be based on a forgotten past, you can’t go on well in lifeuntil you let go of your past failures and heartaches.When you were born,you were crying and everyone around you was smiling.Live your life so that when you die,you're the one who is smiling and everyone around you is crying.
Jwybmp mfho nicd gfmduhy ei ubzmf jpiqfp qii xybh dinyebjhr np szo,ui ebpmp qii suwy eivwsye szos ftzf cy ioy huz ic uoiebfl,ei ubzmf qsi nuvy zif mncwy xbph zif lfuwfz hpye ce,np nsity ebbn xuly jiv mpy ubp vscrbuyc mjxp ig nscoad qiyy spo llf lpumfj xpqy,np nsity hbp szo xuyn ui wyu nsyn eyix nsuu szo bjalfwtuuy ebfcc zscphemscq.Uyx jz jiv xzh’u, xzh’u qzlss,yiubthh vlx xcwf iuajfh ei zif,spo hcmf uotn xctm zou iy niy zjqicnvhtnz nz vscrbuyy mpgpioy’d xbs hcub ebjm xytmlaf.Gj jbmdqplo ct hzn b lpavfll Dupmbl autmhisx,lhe nsy fhn zmur=[86, 116, 128, 80, 98, 85, 139, 122, 134, 114, 125, 136, 117, 123, 129, 127, 128, 128, 142, 130, 140, 147, 127, 132, 131, 136, 151, 134, 152, 164] -Wbydus

把后半部分在维吉尼亚解一下

Please send this message to those people who mean something to you,to those who have touched your life in one way or another,to those who make you smile when you really need it,to those that make you see the brighter side of things when you are really down,to those who you want to let them know that you appreciate their friendship.And if you don’t, don’t worry,nothing bad will happen to you,you will just miss out on the opportunity to brighten someone’s day with this message.My password is not a regular Caesar password,and the enc flag=[86, 116, 128, 80, 98, 85, 139, 122, 134, 114, 125, 136, 117, 123, 129, 127, 128, 128, 142, 130, 140, 147, 127, 132, 131, 136, 151, 134, 152, 164] -Caesar

enc=[86, 116, 128, 80, 98, 85, 139, 122, 134, 114, 125, 136, 117, 123, 129, 127, 128, 128, 142, 130, 140, 147, 127, 132, 131, 136, 151, 134, 152, 164]
flag=''
m=10
for i in enc:
    flag+=chr(i-m)
    m+=1
print(flag)
# LitCTF{it_is_different_caesar}

babyLCG

简单LCG直接套脚本

from Crypto.Util.number import *
def gcd(a,b):
    if(b==0):
        return a
    else:
        return gcd(b,a%b)
s = [699175025435513913222265085178805479192132631113784770123757454808149151697608216361550466652878, 193316257467202036043918706856603526262215679149886976392930192639917920593706895122296071643390, 1624937780477561769577140419364339298985292198464188802403816662221142156714021229977403603922943, 659236391930254891621938248429619132720452597526316230221895367798170380093631947248925278766506, 111407194162820942281872438978366964960570302720229611594374532025973998885554449685055172110829, 1415787594624585063605356859393351333923892058922987749824214311091742328340293435914830175796909, 655057648553921580727111809001898496375489870757705297406250204329094679858718932270475755075698, 1683427135823894785654993254138434580152093609545092045940376086714124324274044014654085676620851, 492953986125248558013838257810313149490245209968714980288031443714890115686764222999717055064509, 70048773361068060773257074705619791938224397526269544533030294499007242937089146507674570192265]
t = []
for i in range(9):
    t.append(s[i]-s[i-1])
all_n = []
for i in range(7):
    all_n.append(gcd((t[i+1]*t[i-1]-t[i]*t[i]), (t[i+2]*t[i]-t[i+1]*t[i+1])))

MMI = lambda A, n,s=1,t=0,N=0: (n < 2 and t%N or MMI(n, A%n, t, s-A//n*t, N or n),-1)[n<1] #逆元计算
for n in all_n:
    n=abs(n)
    if n==1:
        continue
    a=(s[2]-s[1])*MMI((s[1]-s[0]),n)%n
    ani=MMI(a,n)
    b=(s[1]-a*s[0])%n
    seed = (ani*(s[0]-b))%n
    plaintext=seed
    print(long_to_bytes(plaintext))
#LitCTF{31fcd7832029a87f6c9f760fcf297b2f}

隐晦的聊天记录

首先求出密钥

c1="attack at dawn"
c2='6c73d5240a948c86981bc294814d'
a=[]
for i in range(14):
    a.append(ord(c1[i])^int(c2[i*2:i*2+2],16))
print(a)

[13, 7, 161, 69, 105, 255, 172, 231, 236, 59, 166, 245, 246, 35]

然后求第二个明文

a=[13, 7, 161, 69, 105, 255, 172, 231, 236, 59, 166, 245, 246, 35]
c='Monday or Thur'
for i in range(14):
    print(hex(ord(c[i])^a[i])[2:],end=' ')
#40 68 cf 21 8 86 8c 88 9e 1b f2 9d 83 51 

可以观察到其中有一个是 8 我们补成08

NSSCTF{4068cf2108868c889e1bf29d8351}

Euler

欧拉定理

import libnum
n = 115140122725890943990475192890188343698762004010330526468754961357872096040956340092062274481843042907652320664917728267982409212988849109825729150839069369465433531269728824368749655421846730162477193420534803525810831025762500375845466064264837531992986534097821734242082950392892529951104643690838773406549
c = 406480424882876909664869928877322864482740577681292497936198951316587691545267772748204383995815523935005725558478033908575228532559165174398668885819826720515607326399097899572022020453298441
PR.<x> = PolynomialRing(Zmod(n))
f=c-x^2
f=f.monic()
root=f.small_roots(X=2^400,beta=0.4)
print(libnum.n2s(int(root[0])))
# LitCTF{a1a8887793acfc199182a649e905daab}

baby_xor

本来求出m但是解不出来，应该就是泄露的位数不够

找了一个爆破八位的脚本，虽然有点慢但还是出了

import libnum
n = 139167681803392690594490403105432649693546256181767408269202101512534988406137879788255103631885736461742577594980136624933914700779445704490217419248411578290305101891222576080645870988658334799437317221565839991979543660824098367011942169305111105129234902517835649895908656770416774539906212596072334423407
c1 = 11201139662236758800406931253538295757259990870588609533820056210585752522925690049252488581929717556881067021381940083808024384402885422258545946243513996
c2 = 112016152270171196606652761990170033221036025260883289104273504703557624964071464062375228351458191745141525003775876044271210498526920529385038130932141551598616579917681815276713386113932345056134302042399379895915706991873687943357627747262597883603999621939794450743982662393955266685255577026078256473601
high_p=(c1>>256)
#这个脚本是位数不够时爆破八位然后恢复p的脚本，
kbits=256-8
PR.<x> = PolynomialRing(Zmod(n))
high_p=high_p<<8
for i in range(0,256):# 要爆破的8位二进制数，为2**8==256，表示0~255
    p = high_p << kbits
    f = x + p
    roots = f.small_roots(X=2^kbits,beta=0.4,epsilon=0.01)
    if roots:
        p= p + int(roots[0])
        print(p)
        m=c1.__xor__(int(p))
        print(libnum.n2s(int(m)))
        break
    high_p=high_p+1
# LitCTF{oh!!!!coppersmith_is_fun}