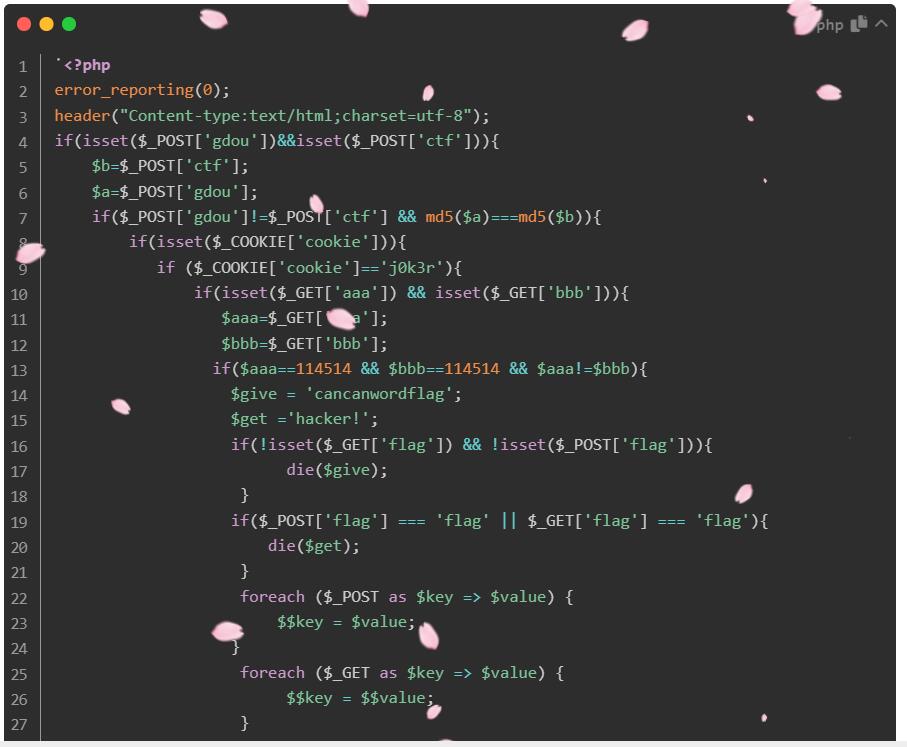
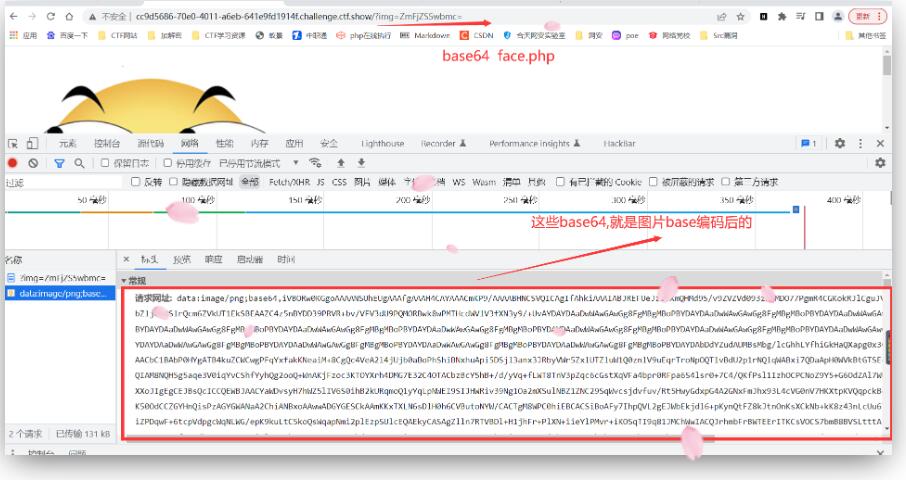
本次round好多交互,这种类型得脚本写的比较少,参考了一些大佬的脚本
ez_enc
ABAABBBAABABAABBABABAABBABAAAABBABABABAAABAAABBAABBBBABBABBABBABABABAABBAABBABAAABBAABBBABABABAAAABBAAABABAABABBABBBABBAAABBBAABABAABBAAAABBBAAAABAABBBAABBABABAABABAAAAABBBBABAABBBBAAAABBBBBAB提示不是培根密码
直接ciphey一把梭
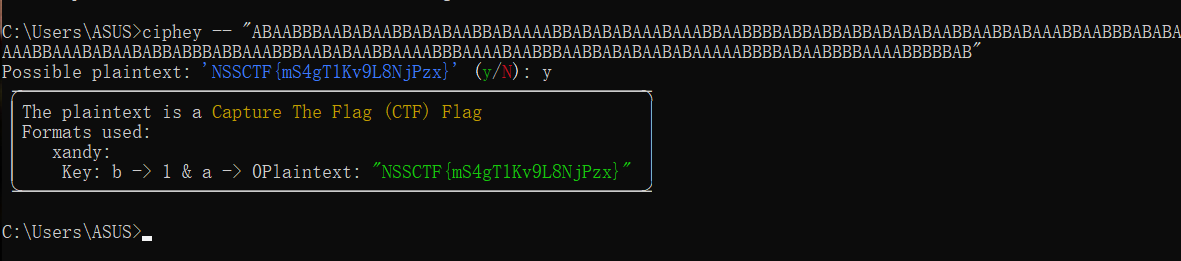
NSSCTF{mS4gT1Kv9L8NjPzx}
或者B–>1,A–>0,然后转文本
ez_signin
题目
from Crypto.Util.number import *
from secret import flag
p = getPrime(512)
q = getPrime(512)
assert p > q
n = p*q
e = 65536
m = bytes_to_long(flag)
num1 = (pow(p,e,n)-pow(q,e,n)) % n
num2 = pow(p-q,e,n)
c = pow(m,e,n)
print("num1=",num1)
print("num2=",num2)
print("n=",n)
print("c=",c)
脚本
分析:
$num1 \equiv p^e - q^e mod n$
$num2 \equiv (p-q)^e \equiv p^e + q^e mod n$
$num1 + num2 \equiv 2p^e mod n$
将上式与n求gcd即可分解n
特殊的地方在e=65536,观察可以得到这里p q都是4k+3型素数,想到是rabin的变式,进行16次rabin算法即可
num1= 24878810498817248549601963074742685387386464942462157441627831559105735510922831745148498491917305807763652117589000468102621763100124920892363322194429534963670648950723660355117500201845429921299091570150674940239532169196783311708023321903390056373346462408338127956230246368885082072149299468189613330701
num2= 56042767418908338314258886089384708269108770192686490541655734563698206477690563665417949934725233235902569236157929677765439019670917433092766376185064198413489357059092974054470881454103094970536553398696049799479326484291184241512583550559743820850066081694272753995204856617490081525492534694894128803854
n= 82787523645374032053495210843370017123931172377557271655638312997792541298388666815392709656552641860759854061080381255745530793945458793925964239003822125725989147047931146084256499955384247979600706446509819528773207269723034851995962510261418309720723966938718829746368418522291444193759059939732595711529
c= 34003458028770944852041095267110206438297243701089262869163250699264377890408968607261710243439051430361829201875786192841340344437449619791066464678110573083728216440444967701968867091815499710925753219016250452889993999986949308467638206737284082995045112478010799884241546145302576780928007895589838096434
e=65536
from Crypto.Util.number import *
import gmpy2
p = GCD(num1+num2,n)
q = n//p
x0=gmpy2.invert(p,q)
x1=gmpy2.invert(q,p)
cs = [c]
for i in range(16):
ps = []
for c2 in cs:
r = pow(c2, (p + 1) // 4, p)
s = pow(c2, (q + 1) // 4, q)
x = (r * x1 * q + s * x0 * p) % n
y = (r * x1 * q - s * x0 * p) % n
if x not in ps:
ps.append(x)
if n - x not in ps:
ps.append(n - x)
if y not in ps:
ps.append(y)
if n - y not in ps:
ps.append(n - y)
cs = ps
for m in ps:
flag = long_to_bytes(m)
if b"NSS" in flag:
print(flag)
break
# NSSCTF{f594e3cd-2b9f-4fbf-992b-40e51897798e}MyMessage
交互式得低指加密广播攻击
from Crypto.Util.number import *
import gmpy2
from pwn import *
from functools import reduce
e = 127
context(log_level="debug")
sh = remote('node4.anna.nssctf.cn',28154)
#命令简写化
sla = lambda delim,data :sh.sendlineafter(delim, data)
ru = lambda delims :sh.recvuntil(delims,drop=True) #接收数据直到delims截止,Ture是不舍弃delims
n=[]
c=[]
for i in range(0,64):
sla("Input message:",str(1))
ru("n: ")
n.append(int(ru('\n'),10))
ru("Token: ")
c.append(int(ru('\n'),16))
#print(n,hex(c[0]))
def CRT(mi, ai):
assert (reduce(gmpy2.gcd, mi) == 1)
assert (isinstance(mi, list) and isinstance(ai, list))
M = reduce(lambda x, y: x * y, mi)
ai_ti_Mi = [a * (M // m) * gmpy2.invert(M // m, m) for (m, a) in zip(mi, ai)]
return reduce(lambda x, y: x + y, ai_ti_Mi) % M
m=CRT(n,c)
M = long_to_bytes(int(gmpy2.iroot(gmpy2.mpz(m),e)[0]))
print(M)
#NSSCTF{c05c93d8-20de-433d-8202-3d8262f31bc0}ez_fac
题目
from Crypto.Util.number import *
import random
from secret import flag,a0,a1,b0,b1
p = getPrime(512)
q = getPrime(512)
e = getPrime(128)
n = p*q
assert pow(a0,2) + e * pow(b0,2) == n
assert pow(a1,2) + e * pow(b1,2) == n
m = bytes_to_long(flag)
c = pow(m,e,n)
print("c=",c)
print("n=",n)
print("a0=",a0)
print("a1=",a1)
print("b0=",b0)
print("b1=",b1)
脚本
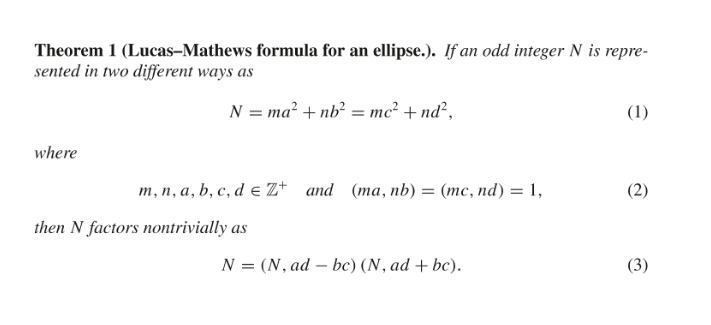
根据这个论文内容
p=gcd(n,a0b1-a1b0)
import gmpy2
import libnum
c= 96496391731007518897413814188008837720590769169211349809877119278985060969026829802572421817888265342360728332919792452440257688078830103285268813765013959424069955273085274413461221917705521199430165698638444416803428336335625130197212968481383466732608552580369509828042748166516923158871160383760272230369
n= 141463050429131153304507639706519453416500899516192888621725244147759861249532811353612272262251738001327556271543066487909395260247788929891078913533139738961651278577096628336832901751330655366664417508431204965468392923655570929035177816875190252113101286809899310780398065797539784080443884076015636565653
a0= 11893824045660468459077133582738838417842593231821092698714037336632395431658199472925765178830611973650766264632249341194655235407390022682840914711732709
a1= 11893824045660468459077133226975764782410316195614509064302075133171334301975298793502355669613006211742097696027917390142838498212910217928927499841689611
b0= 72637686840312330318324544577081835760892845722490802999295104254521408572725988691542710106291484785108130437411841119266
b1= 199793516086267640308411342691103208215027194945128541613925289581349442759392411456693594969683135744315154264882943680006
p=gmpy2.gcd(n,a0*b1-a1*b0)
q=n//p
e=(pow(a0,2)-pow(a1,2))//(pow(b1,2)-pow(b0,2))
phi=(p-1)*(q-1)
d=gmpy2.invert(e,phi)
m=pow(c,d,n)
print(libnum.n2s(int(m)))
#NSSCTF{e2e87199-7473-4548-bc29-0e1ddccd1adb}MyGame
题目
from Crypto.Util.number import *
import os
import random
import string
flag = os.getenv('FLAG')
def menu():
print('''=---menu---=
1. Guess
2. Encrypt
''')
p = getPrime(512)
q = getPrime(512)
n = p*q
def randommsg():
return ''.join(random.choices(string.ascii_lowercase+string.digits, k=30))
mymsg = randommsg()
def guess():
global mymsg
msg = input()
if msg == mymsg:
print(flag)
else:
print(mymsg)
mymsg = randommsg()
def encrypt():
e = random.getrandbits(8)
c = pow(bytes_to_long(mymsg.encode()), e, n)
print(f'Cipher_{e}: {c}')
def main():
print(f'n: {n}')
while True:
opt = int(input())
if opt == 1:
guess()
elif opt == 2:
encrypt()
main()脚本
from pwn import *
import re
import binascii, gmpy2
import libnum
# ------------ 交互部分 ------------
host = 'node1.anna.nssctf.cn'
port = 28935
conn = remote(host, port)
data1 = conn.recvline().decode()
n = int(re.findall(r'n: (\d+)', data1)[0])
def interact_with_server(conn):
conn.sendline("2")
data1 = conn.recvline().decode()
print(data1)
e, c = re.findall(r'Cipher_(\d+): (\d+)', data1)[0]
e = int(e)
c = int(c)
return e, c
#共模攻击
#共模攻击函数
def rsa_gong_N_def(e1,e2,c1,c2,n):
e1, e2, c1, c2, n=int(e1),int(e2),int(c1),int(c2),int(n)
s = gmpy2.gcdext(e1, e2)
s1 = s[1]
s2 = s[2]
if s1 < 0:
s1 = - s1
c1 = gmpy2.invert(c1, n)
elif s2 < 0:
s2 = - s2
c2 = gmpy2.invert(c2, n)
m = (pow(c1,s1,n) * pow(c2 ,s2 ,n)) % n
return int(m)
e1,c1=interact_with_server(conn)
e2,c2=interact_with_server(conn)
m = rsa_gong_N_def(e1, e2, c1, c2, n)
flag = libnum.n2s(int(m))
conn.sendline("1")
conn.sendline(flag)
print(conn.recvline().decode())
#NSSCTF{0d11d1d2-22c5-41ec-88c8-b3e70cb61a0b}