ECC椭圆曲线

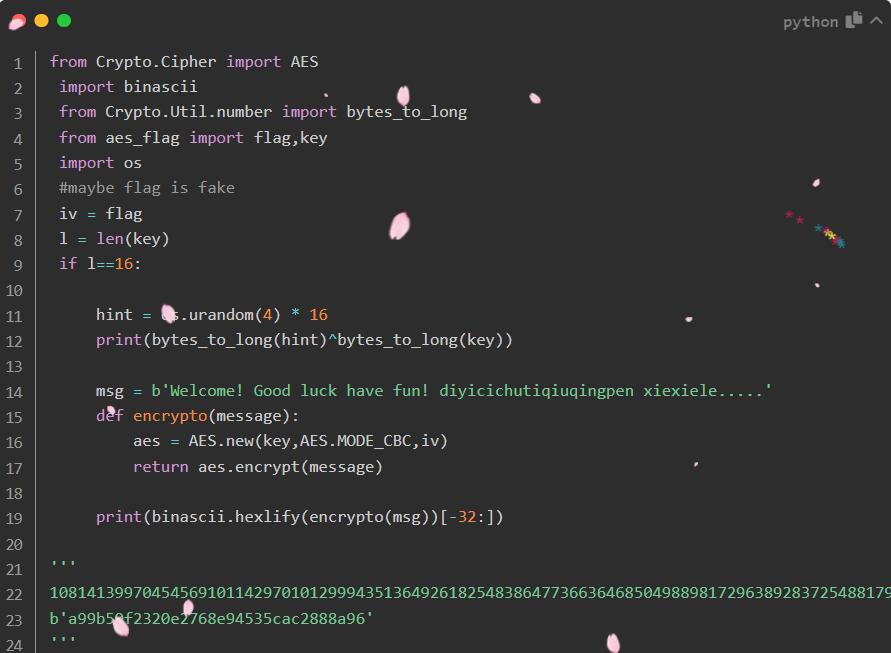
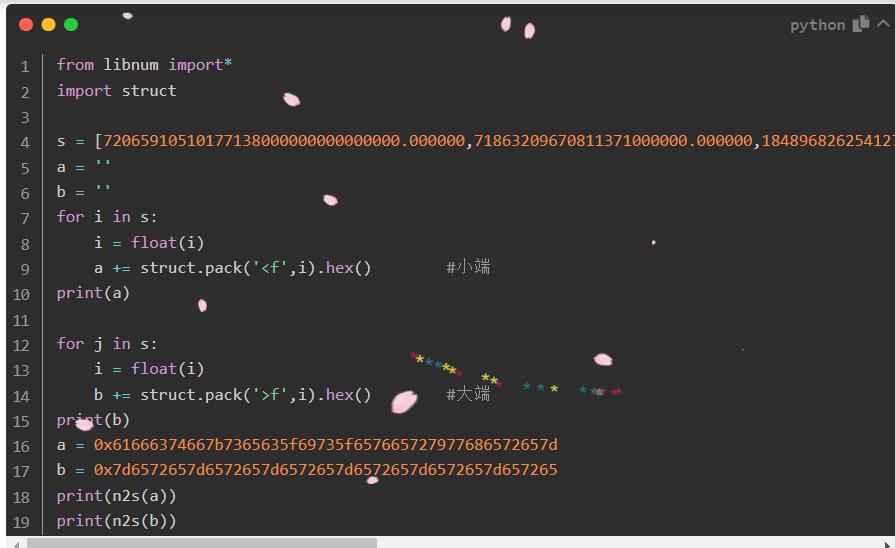
参考la佬博客 Lazzaro @ https://lazzzaro.github.io

椭圆曲线的定义式：y2+axy+by=x3+cx2+dx+e

一般方程：y2+a1xy+a3y=x3+a2x2+a4x+a6

最常用方程（维尔斯特拉斯标准形式）

y2=x3+ax+b

Smart’s attack

适用情况：E.order()=pE.order()=p。

p = 
A = 
B = 
E = EllipticCurve(GF(p),[A,B])
P = E(,)
Q = E(,)
def SmartAttack(P,Q,p):
    E = P.curve()
    Eqp = EllipticCurve(Qp(p, 2), [ ZZ(t) + randint(0,p)*p for t in E.a_invariants() ])

    P_Qps = Eqp.lift_x(ZZ(P.xy()[0]), all=True)
    for P_Qp in P_Qps:
        if GF(p)(P_Qp.xy()[1]) == P.xy()[1]:
            break

    Q_Qps = Eqp.lift_x(ZZ(Q.xy()[0]), all=True)
    for Q_Qp in Q_Qps:
        if GF(p)(Q_Qp.xy()[1]) == Q.xy()[1]:
            break

    p_times_P = p*P_Qp
    p_times_Q = p*Q_Qp

    x_P,y_P = p_times_P.xy()
    x_Q,y_Q = p_times_Q.xy()

    phi_P = -(x_P/y_P)
    phi_Q = -(x_Q/y_Q)
    k = phi_Q/phi_P
    return ZZ(k)

r = SmartAttack(P, Q, p)
print(r)

ECDLP

CDLP即椭圆曲线上的离散对数问题（The Elliptic Curve Discrete Logarithm Problem）。

椭圆曲线上离散对数问题ECDLP定义如下：给定素数 pp 和椭圆曲线 EE，对 Q=kPQ=kP，在已知 P,QP,Q 的情况下求出小于 pp 的正整数 kk。可以证明由 kk 和 PP 计算 QQ 比较容易，而由 QQ 和 PP 计算 kk 则比较困难。将椭圆曲线中的加法运算与离散对数中的模乘运算相对应，将椭圆曲线中的乘法运算与离散对数中的模幂运算相对应，我们就可以建立基于椭圆曲线的对应的密码体制。

#Sage Code 1
p = 
a = 
b = 
E = EllipticCurve(GF(p),[a,b])
P = E(, ) 
Q = E(, ) 
k = discrete_log(Q, P, operation='+') 
print(k)

#Sage Code 2
p = 
a = 
b = 
E = EllipticCurve(GF(p),[a,b])
P = E(, ) 
Q = E(, ) 
k = P.discrete_log(Q)
print(k)

Pohlig-Hellman算法

#Sage Code 1
p = 
a = 
b = 
gx = 
gy = 
px = 
py = 

E = EllipticCurve(GF(p), [a, b])
G = E(gx, gy)
n = E.order()
QA = E(px, py)

factors = list(factor(n))
m = 1
moduli = []
remainders = []

print(f"[+] Running Pohlig Hellman")
print(factors)

for i, j in factors:
    if i > 10**9:
        print(i)
        break
    mod = i**j
    g2 = G*(n//mod)
    q2 = QA*(n//mod)
    r = discrete_log(q2, g2, operation='+')
    remainders.append(r)
    moduli.append(mod)
    m *= mod

r = crt(remainders, moduli)
print(r)

#Sage Code 2
E = EllipticCurve(GF(p), [a, b])
P = E()
Q = E()

factors, exponents = zip(*factor(E.order()))
primes = [factors[i] ^ exponents[i] for i in range(len(factors))][:-2]
print(primes)
dlogs = []
for fac in primes:
	t = int(int(P.order()) // int(fac))
	dlog = discrete_log(t*Q,t*P,operation="+")
	dlogs += [dlog]
	print("factor: "+str(fac)+", Discrete Log: "+str(dlog)) #calculates discrete logarithm for each prime order

l = crt(dlogs,primes)
print(l)