相关网址
https://blog.csdn.net/q851579181q/article/details/90645041https://www.jianshu.com/p/d8d2ce53041b1.已知m的高位
题目
n=0x2519834a6cc3bf25d078caefc5358e41c726a7a56270e425e21515d1b195b248b82f4189a0b621694586bb254e27010ee4376a849bb373e5e3f2eb622e3e7804d18ddb897463f3516b431e7fc65ec41c42edf736d5940c3139d1e374aed1fc3b70737125e1f540b541a9c671f4bf0ded798d727211116eb8b86cdd6a29aefcc7L
e=3
m=random.getrandbits(512)
c=pow(m,e,n)=0x1f6f6a8e61f7b5ad8bef738f4376a96724192d8da1e3689dec7ce5d1df615e0910803317f9bafb6671ffe722e0292ce76cca399f2af1952dd31a61b37019da9cf27f82c3ecd4befc03c557efe1a5a29f9bb73c0239f62ed951955718ac0eaa3f60a4c415ef064ea33bbd61abe127c6fc808c0edb034c52c45bd20a219317fb75L
((m>>72)<<72)=0xb11ffc4ce423c77035280f1c575696327901daac8a83c057c453973ee5f4e508455648886441c0f3393fe4c922ef1c3a6249c12d21a000000000000000000Lsage解密脚本
n = 0x2519834a6cc3bf25d078caefc5358e41c726a7a56270e425e21515d1b195b248b82f4189a0b621694586bb254e27010ee4376a849bb373e5e3f2eb622e3e7804d18ddb897463f3516b431e7fc65ec41c42edf736d5940c3139d1e374aed1fc3b70737125e1f540b541a9c671f4bf0ded798d727211116eb8b86cdd6a29aefcc7
e = 3
m = randrange(n)
c = pow(m, e, n)
beta = 1
epsilon = beta^2/7
nbits = n.nbits()
kbits = floor(nbits*(beta^2/e-epsilon))
mbar = 0xb11ffc4ce423c77035280f1c575696327901daac8a83c057c453973ee5f4e508455648886441c0f3393fe4c922ef1c3a6249c12d21a000000000000000000
c = 0x1f6f6a8e61f7b5ad8bef738f4376a96724192d8da1e3689dec7ce5d1df615e0910803317f9bafb6671ffe722e0292ce76cca399f2af1952dd31a61b37019da9cf27f82c3ecd4befc03c557efe1a5a29f9bb73c0239f62ed951955718ac0eaa3f60a4c415ef064ea33bbd61abe127c6fc808c0edb034c52c45bd20a219317fb75
print ("upper %d bits (of %d bits) is given" % (nbits-kbits, nbits))
PR.<x> = PolynomialRing(Zmod(n))
f = (mbar + x)^e - c
x0 = f.small_roots(X=2^kbits, beta=1)[0] # find root < 2^kbits with factor = n1
print (mbar + x0)2.p高位攻击
题目
n=0x5894f869d1aecee379e2cb60ff7314d18dbd383e0c9f32e7f7b4dc8bd47535d4f3512ce6a23b0251049346fede745d116ba8d27bcc4d7c18cfbd86c7d065841788fcd600d5b3ac5f6bb1e111f265994e550369ddd86e20f615606bf21169636d153b6dfee4472b5a3cb111d0779d02d9861cc724d389eb2c07a71a7b3941da7dL
e=65537
m=random.getrandbits(512)
c=pow(m,e,n)=0x284a601c3321fd882d3b64ae27fb587d1714bc18aecc3293169861bcf17678a6e83947aba4f165f22a712ed42e43c66cf70eb1df4d73dd3adf1754f627b1b3ca25b76b3a595369c36b1f5635cd3efe5924539757e74840224eec238534ead0bcbdce26eb018aa33516d22790240c7576cb5a09d3f69bcf2795a3a353db7c8bedL
((p>>128)<<128)=0x5d33504b4e3bd2ffb628b5c447c4a7152a9f37dc4bcc8f376f64000fa96eb97c0af445e3b2c03926a4aa4542918c601000000000000000000000000000000000Lsage解密脚本
n = 0x5894f869d1aecee379e2cb60ff7314d18dbd383e0c9f32e7f7b4dc8bd47535d4f3512ce6a23b0251049346fede745d116ba8d27bcc4d7c18cfbd86c7d065841788fcd600d5b3ac5f6bb1e111f265994e550369ddd86e20f615606bf21169636d153b6dfee4472b5a3cb111d0779d02d9861cc724d389eb2c07a71a7b3941da7dL
p_fake = 0x5d33504b4e3bd2ffb628b5c447c4a7152a9f37dc4bcc8f376f64000fa96eb97c0af445e3b2c03926a4aa4542918c601000000000000000000000000000000000
pbits = p_fake.nbits()
kbits = 128 #p失去的低位
pbar = p_fake & (2^pbits-2^kbits)
print ("upper %d bits (of %d bits) is given" % (pbits-kbits, pbits))
PR.<x> = PolynomialRing(Zmod(n))
f = x + pbar
x0 = f.small_roots(X=2^kbits, beta=0.4)[0] # find root < 2^kbits with factor >= n^0.3
print (x0 + pbar)3、已知私钥d的512位的低位
题目
n=0xd463feb999c9292e25acd7f98d49a13413df2c4e74820136e739281bb394a73f2d1e6b53066932f50a73310360e5a5c622507d8662dadaef860b3266222129fd645eb74a0207af9bd79a9794f4bd21f32841ce9e1700b0b049cfadb760993fcfc7c65eca63904aa197df306cad8720b1b228484629cf967d808c13f6caef94a9L
e=3
m=random.getrandbits(512)
c=pow(m,e,n)=0xcaeeb38516d642a19550fa863173f4695c3b44bd5a5554b1e93cfb690d5c1de531b7f1187f7d8c8c11da38af025f19d393033d0ca801e15d6d8441098485f13ab988d09ef1f4f5a735e19780c823cf77415884c33a1f7908cf4229874c082eb7ceb776bafb182b86fdabd29b07bcb8e3f2f50ee4cc0f323e8d9ce320139bcd27L
d=invmod(e,(p-1)*(q-1))
d&((1<<512)-1)=0x603d033f2ef6c759aec839f132a45215fc8a635b757f3951a731fe60bc6729b3bcf819b57abfcaba3a93e9edef766c0d499cad3f7adb306bcf1645cfb63400e3L
long_to_bytes(m).encode('hex')=???sage解密脚本
def partial_p(p0, kbits, n):
PR.<x> = PolynomialRing(Zmod(n))
nbits = n.nbits()
f = 2^kbits*x + p0
f = f.monic()
roots = f.small_roots(X=2^(nbits//2-kbits), beta=0.3) # find root < 2^(nbits//2-kbits) with factor >= n^0.3
if roots:
x0 = roots[0]
p = gcd(2^kbits*x0 + p0, n)
return ZZ(p)
def find_p(d0, kbits, e, n):
X = var('X')
for k in range(1, e+1):
results = solve_mod([e*d0*X - k*X*(n-X+1) + k*n == X], 2^kbits)
for x in results:
p0 = ZZ(x[0])
p = partial_p(p0, kbits, n)
if p:
return p
if __name__ == '__main__':
n = 0xd463feb999c9292e25acd7f98d49a13413df2c4e74820136e739281bb394a73f2d1e6b53066932f50a73310360e5a5c622507d8662dadaef860b3266222129fd645eb74a0207af9bd79a9794f4bd21f32841ce9e1700b0b049cfadb760993fcfc7c65eca63904aa197df306cad8720b1b228484629cf967d808c13f6caef94a9
e = 3
d = 0x603d033f2ef6c759aec839f132a45215fc8a635b757f3951a731fe60bc6729b3bcf819b57abfcaba3a93e9edef766c0d499cad3f7adb306bcf1645cfb63400e3
beta = 0.5
epsilon = beta^2/7
nbits = n.nbits()
print ("nbits:%d:"%(nbits))
#kbits = floor(nbits*(beta^2+epsilon))
kbits = nbits - d.nbits()-1
print ("kbits:%d"%(kbits))
d0 = d & (2^kbits-1)
print ("lower %d bits (of %d bits) is given" % (kbits, nbits))
p = find_p(d0, kbits, e, n)
print ("found p: %d" % p)
q = n//p
print (d)
print (inverse_mod(e, (p-1)*(q-1)))4、 低加密指数广播攻击
题目
e=3
m=random.getrandbits(512)
n1=0x5797fdb74bcea6788212fb2c32c5d98d308c617f893d1f375d0e611b424d5656df4465772e278c25e7d1d5fd73b0fdfdac4a786a11403d239a2f84dc77a46c1108219eed98567605ab29ffdeef10594863bb49d45d41c1f3925d6a33bb34205321ab03d906e2d89c2153e76f2ad185bac9fb26099910dd19cf3be35ec7e01df5L
c1=pow(m,e,n1)=0x25e206422ea328f1b295dd121970b874b002789b2419a57584b2f1a682a36312a45efe22bb68694b9c9dfdc63c4f10b746a4a2893b29f918d90cb5129d52e66babf7f8516c44cd33ee27d2cf2968e0002ab2b711387d8f111315bd23d3f92073634ed6e57fa9b56d14104f75336f46c6dd43fbac810a6337a7ad3f60890873bL
n2=0x50998a3cf7f86a3044fe3c1fda2f6df7050383833279ebdbfe943f83faae3ada1bb6e684e48efd0487056849d47552d8052144364a72324b038ea73812960015c678c4e903e25515d874d1435761f20d1d6a066d2b70651c051dc157d2183d91ed6e7ae25d4adb0ce04833b816f96c5fd718c687474cacca6ad1dcc85db07e89L
c2=pow(m,e,n2)=0x448f88bec6795e11b06a7810faf617931bc6d99d1628cafecff1e933154ce575caaf752c3daf50b288ad7759ea8133f7dc9ca42a1b950eb8d538f98e00a4f3ad6bb0d6a9ad5d042d6db710c060bb72aa13065986d8dfb800409c08e4cdee471bc7ef31a6e3e2027ecb8ea9fb9b19440c5272fecf04aefdf2dbeafd994589c09fL
n3=0x15ed9002077c66e48a6fc80ce744f16b87e237ddd9a4efb4ffa2f9f89d09af382dddfc259dbf932728c23757957638f3ec9327fc0eaf3fd5d72b91c714798ca1459dfdf6c7505eb6e39f26624431239b6daa7bbaa6c5aad3dc3bf6b377923781ab5c221c195115d39c477c0561d5c769c17583c5b66d5f21f6683cea2670215bL
c3=pow(m,e,n3)=0xc9ddbb9478d0b64086091aac64efd51eb37b5067feb380995d39a917c0c927b26902f06dc449b53d80cd59c5d912fb5a5f45b223278919ae1ce449f4db7afbc252f16247129ea68dc6011093da6b11356591a9e8c0e10057e9d733712a6e0caafc462e9b2d07fb2aa3a451403a7f84de3504a60e72872df20bc244a0f1c837bL
long_to_bytes(m).encode('hex')=???python脚本
from struct import pack,unpack
import zlib
import gmpy
def my_parse_number(number):
string = "%x" % number
erg = []
while string != '':
erg = erg + [chr(int(string[:2], 16))]
string = string[2:]
return ''.join(erg)
def extended_gcd(a, b):
x,y = 0, 1
lastx, lasty = 1, 0
while b:
a, (q, b) = b, divmod(a,b)
x, lastx = lastx-q*x, x
y, lasty = lasty-q*y, y
return (lastx, lasty, a)
def chinese_remainder_theorem(items):
N = 1
for a, n in items:
N *= n
result = 0
for a, n in items:
m = N//n
r, s, d = extended_gcd(n, m)
if d != 1:
N=N/n
continue
result += a*s*m
return result % N, N
sessions=[{"c": 0x25e206422ea328f1b295dd121970b874b002789b2419a57584b2f1a682a36312a45efe22bb68694b9c9dfdc63c4f10b746a4a2893b29f918d90cb5129d52e66babf7f8516c44cd33ee27d2cf2968e0002ab2b711387d8f111315bd23d3f92073634ed6e57fa9b56d14104f75336f46c6dd43fbac810a6337a7ad3f60890873b, "e": 3, "n":0x5797fdb74bcea6788212fb2c32c5d98d308c617f893d1f375d0e611b424d5656df4465772e278c25e7d1d5fd73b0fdfdac4a786a11403d239a2f84dc77a46c1108219eed98567605ab29ffdeef10594863bb49d45d41c1f3925d6a33bb34205321ab03d906e2d89c2153e76f2ad185bac9fb26099910dd19cf3be35ec7e01df5},
{"c":0x448f88bec6795e11b06a7810faf617931bc6d99d1628cafecff1e933154ce575caaf752c3daf50b288ad7759ea8133f7dc9ca42a1b950eb8d538f98e00a4f3ad6bb0d6a9ad5d042d6db710c060bb72aa13065986d8dfb800409c08e4cdee471bc7ef31a6e3e2027ecb8ea9fb9b19440c5272fecf04aefdf2dbeafd994589c09f , "e": 3, "n":0x50998a3cf7f86a3044fe3c1fda2f6df7050383833279ebdbfe943f83faae3ada1bb6e684e48efd0487056849d47552d8052144364a72324b038ea73812960015c678c4e903e25515d874d1435761f20d1d6a066d2b70651c051dc157d2183d91ed6e7ae25d4adb0ce04833b816f96c5fd718c687474cacca6ad1dcc85db07e89 },
{"c":0xc9ddbb9478d0b64086091aac64efd51eb37b5067feb380995d39a917c0c927b26902f06dc449b53d80cd59c5d912fb5a5f45b223278919ae1ce449f4db7afbc252f16247129ea68dc6011093da6b11356591a9e8c0e10057e9d733712a6e0caafc462e9b2d07fb2aa3a451403a7f84de3504a60e72872df20bc244a0f1c837b , "e": 3, "n":0x15ed9002077c66e48a6fc80ce744f16b87e237ddd9a4efb4ffa2f9f89d09af382dddfc259dbf932728c23757957638f3ec9327fc0eaf3fd5d72b91c714798ca1459dfdf6c7505eb6e39f26624431239b6daa7bbaa6c5aad3dc3bf6b377923781ab5c221c195115d39c477c0561d5c769c17583c5b66d5f21f6683cea2670215b }]
data = []
for session in sessions:
e=session['e']
n=session['n']
msg=session['c']
data = data + [(msg, n)]
print ("Please wait, performing CRT")
x, n = chinese_remainder_theorem(data)
e=session['e']
realnum = gmpy.mpz(x).root(e)[0].digits()
print (my_parse_number(int(realnum)).encode("UTF-8").hex())5、明文c存在线性关系,Related Message Attack 和 RSA Padding Attack
题目
n=0xf9526aad4d41c9b28f8bae279c7ef6b07d729d1f56e530219851f656ad521218815bdccb15167a25633a2f76969fccd3fe1ef379ded08d1a9c3307f680e952956d2b3d04cc50040efb30e40bf2562aae4b05b8ec0d5e0e0ea5fdc1b00b80dee9b6de1d77d41d8d040d3465c89133d9af23b1d43f57e70606e3433d35a47e2edL
e=3
m=random.getrandbits(512)
c=pow(m,e,n)=0x798841c574b7c88ce1430d4b02bac01fc9368c71a7966176b22f9dc2e0c2f6d4d5b8a9e10dbcaa4584e667ef1afd213b78c2bdc16ba5ab909c2de2fe5a7a5fa36a390bdccf794451cd9db8489ed7870efa4a4d7d1cacacfec92e81f6bb955a4ef5d71d80631c0726d22ec3d5b115de7ff42f22e67854b59ed816e06485ab523L
x=pow(m+1,e,n)=0xe92c4c99052fa3c4bb5e54477b0afe8e18da37255269f070ffa6824492a87153e428fa4ed839b7f3249966259a0c88641185594fc2fa4881cf32b7af5b18baa6f5200453ee80e38c74dbeb90f32118e4f33e636a808e44f27e09286d109ee8f41765ad64c7afea9775974d78a80e0977a37689c7f15a23a83a87b1f5bdbcdecL
long_to_bytes(m).encode('hex')=???python脚本
import gmpy2
import functools
def getM2(a,b,c1,c2,n):
a3 = pow(a,3,n)
b3 = pow(b,3,n)
first = c1-a3*c2+2*b3
first = first % n
second = 3*b*(a3*c2-b3)
second = second % n
third = second*gmpy2.invert(first,n)
third = third % n
fourth = (third+b)*gmpy2.invert(a,n)
return fourth % n
a=1
b=-1
padding2=b
n=0xf9526aad4d41c9b28f8bae279c7ef6b07d729d1f56e530219851f656ad521218815bdccb15167a25633a2f76969fccd3fe1ef379ded08d1a9c3307f680e952956d2b3d04cc50040efb30e40bf2562aae4b05b8ec0d5e0e0ea5fdc1b00b80dee9b6de1d77d41d8d040d3465c89133d9af23b1d43f57e70606e3433d35a47e2ed
c1=0x798841c574b7c88ce1430d4b02bac01fc9368c71a7966176b22f9dc2e0c2f6d4d5b8a9e10dbcaa4584e667ef1afd213b78c2bdc16ba5ab909c2de2fe5a7a5fa36a390bdccf794451cd9db8489ed7870efa4a4d7d1cacacfec92e81f6bb955a4ef5d71d80631c0726d22ec3d5b115de7ff42f22e67854b59ed816e06485ab523
c2=0xe92c4c99052fa3c4bb5e54477b0afe8e18da37255269f070ffa6824492a87153e428fa4ed839b7f3249966259a0c88641185594fc2fa4881cf32b7af5b18baa6f5200453ee80e38c74dbeb90f32118e4f33e636a808e44f27e09286d109ee8f41765ad64c7afea9775974d78a80e0977a37689c7f15a23a83a87b1f5bdbcdec
m = getM2(a,b,c1,c2,n)-padding2
print (m)6、私钥d 较小时,满足 d<N^0.292,Boneh and Durfee attack
题目
[+]Generating challenge 6
[+]n=0xbadd260d14ea665b62e7d2e634f20a6382ac369cd44017305b69cf3a2694667ee651acded7085e0757d169b090f29f3f86fec255746674ffa8a6a3e1c9e1861003eb39f82cf74d84cc18e345f60865f998b33fc182a1a4ffa71f5ae48a1b5cb4c5f154b0997dc9b001e441815ce59c6c825f064fdca678858758dc2cebbc4d27L
[+]d=random.getrandbits(1024*0.270)
[+]e=invmod(d,phin)
[+]hex(e)=0x11722b54dd6f3ad9ce81da6f6ecb0acaf2cbc3885841d08b32abc0672d1a7293f9856db8f9407dc05f6f373a2d9246752a7cc7b1b6923f1827adfaeefc811e6e5989cce9f00897cfc1fc57987cce4862b5343bc8e91ddf2bd9e23aea9316a69f28f407cfe324d546a7dde13eb0bd052f694aefe8ec0f5298800277dbab4a33bbL
[+]m=random.getrandbits(512)
[+]c=pow(m,e,n)=0xe3505f41ec936cf6bd8ae344bfec85746dc7d87a5943b3a7136482dd7b980f68f52c887585d1c7ca099310c4da2f70d4d5345d3641428797030177da6cc0d41e7b28d0abce694157c611697df8d0add3d900c00f778ac3428f341f47ecc4d868c6c5de0724b0c3403296d84f26736aa66f7905d498fa1862ca59e97f8f866cL
[-]long_to_bytes(m).encode('hex')=python脚本
import time
############################################
# Config
##########################################
"""
Setting debug to true will display more informations
about the lattice, the bounds, the vectors...
"""
debug = True
"""
Setting strict to true will stop the algorithm (and
return (-1, -1)) if we don't have a correct
upperbound on the determinant. Note that this
doesn't necesseraly mean that no solutions
will be found since the theoretical upperbound is
usualy far away from actual results. That is why
you should probably use `strict = False`
"""
strict = False
"""
This is experimental, but has provided remarkable results
so far. It tries to reduce the lattice as much as it can
while keeping its efficiency. I see no reason not to use
this option, but if things don't work, you should try
disabling it
"""
helpful_only = True
dimension_min = 7 # stop removing if lattice reaches that dimension
############################################
# Functions
##########################################
# display stats on helpful vectors
def helpful_vectors(BB, modulus):
nothelpful = 0
for ii in range(BB.dimensions()[0]):
if BB[ii,ii] >= modulus:
nothelpful += 1
print nothelpful, "/", BB.dimensions()[0], " vectors are not helpful"
# display matrix picture with 0 and X
def matrix_overview(BB, bound):
for ii in range(BB.dimensions()[0]):
a = ('%02d ' % ii)
for jj in range(BB.dimensions()[1]):
a += '0' if BB[ii,jj] == 0 else 'X'
if BB.dimensions()[0] < 60:
a += ' '
if BB[ii, ii] >= bound:
a += '~'
print a
# tries to remove unhelpful vectors
# we start at current = n-1 (last vector)
def remove_unhelpful(BB, monomials, bound, current):
# end of our recursive function
if current == -1 or BB.dimensions()[0] <= dimension_min:
return BB
# we start by checking from the end
for ii in range(current, -1, -1):
# if it is unhelpful:
if BB[ii, ii] >= bound:
affected_vectors = 0
affected_vector_index = 0
# let's check if it affects other vectors
for jj in range(ii + 1, BB.dimensions()[0]):
# if another vector is affected:
# we increase the count
if BB[jj, ii] != 0:
affected_vectors += 1
affected_vector_index = jj
# level:0
# if no other vectors end up affected
# we remove it
if affected_vectors == 0:
print "* removing unhelpful vector", ii
BB = BB.delete_columns([ii])
BB = BB.delete_rows([ii])
monomials.pop(ii)
BB = remove_unhelpful(BB, monomials, bound, ii-1)
return BB
# level:1
# if just one was affected we check
# if it is affecting someone else
elif affected_vectors == 1:
affected_deeper = True
for kk in range(affected_vector_index + 1, BB.dimensions()[0]):
# if it is affecting even one vector
# we give up on this one
if BB[kk, affected_vector_index] != 0:
affected_deeper = False
# remove both it if no other vector was affected and
# this helpful vector is not helpful enough
# compared to our unhelpful one
if affected_deeper and abs(bound - BB[affected_vector_index, affected_vector_index]) < abs(bound - BB[ii, ii]):
print "* removing unhelpful vectors", ii, "and", affected_vector_index
BB = BB.delete_columns([affected_vector_index, ii])
BB = BB.delete_rows([affected_vector_index, ii])
monomials.pop(affected_vector_index)
monomials.pop(ii)
BB = remove_unhelpful(BB, monomials, bound, ii-1)
return BB
# nothing happened
return BB
"""
Returns:
* 0,0 if it fails
* -1,-1 if `strict=true`, and determinant doesn't bound
* x0,y0 the solutions of `pol`
"""
def boneh_durfee(pol, modulus, mm, tt, XX, YY):
"""
Boneh and Durfee revisited by Herrmann and May
finds a solution if:
* d < N^delta
* |x| < e^delta
* |y| < e^0.5
whenever delta < 1 - sqrt(2)/2 ~ 0.292
"""
# substitution (Herrman and May)
PR.<u, x, y> = PolynomialRing(ZZ)
Q = PR.quotient(x*y + 1 - u) # u = xy + 1
polZ = Q(pol).lift()
UU = XX*YY + 1
# x-shifts
gg = []
for kk in range(mm + 1):
for ii in range(mm - kk + 1):
xshift = x^ii * modulus^(mm - kk) * polZ(u, x, y)^kk
gg.append(xshift)
gg.sort()
# x-shifts list of monomials
monomials = []
for polynomial in gg:
for monomial in polynomial.monomials():
if monomial not in monomials:
monomials.append(monomial)
monomials.sort()
# y-shifts (selected by Herrman and May)
for jj in range(1, tt + 1):
for kk in range(floor(mm/tt) * jj, mm + 1):
yshift = y^jj * polZ(u, x, y)^kk * modulus^(mm - kk)
yshift = Q(yshift).lift()
gg.append(yshift) # substitution
# y-shifts list of monomials
for jj in range(1, tt + 1):
for kk in range(floor(mm/tt) * jj, mm + 1):
monomials.append(u^kk * y^jj)
# construct lattice B
nn = len(monomials)
BB = Matrix(ZZ, nn)
for ii in range(nn):
BB[ii, 0] = gg[ii](0, 0, 0)
for jj in range(1, ii + 1):
if monomials[jj] in gg[ii].monomials():
BB[ii, jj] = gg[ii].monomial_coefficient(monomials[jj]) * monomials[jj](UU,XX,YY)
# Prototype to reduce the lattice
if helpful_only:
# automatically remove
BB = remove_unhelpful(BB, monomials, modulus^mm, nn-1)
# reset dimension
nn = BB.dimensions()[0]
if nn == 0:
print "failure"
return 0,0
# check if vectors are helpful
if debug:
helpful_vectors(BB, modulus^mm)
# check if determinant is correctly bounded
det = BB.det()
bound = modulus^(mm*nn)
if det >= bound:
print "We do not have det < bound. Solutions might not be found."
print "Try with highers m and t."
if debug:
diff = (log(det) - log(bound)) / log(2)
print "size det(L) - size e^(m*n) = ", floor(diff)
if strict:
return -1, -1
else:
print "det(L) < e^(m*n) (good! If a solution exists < N^delta, it will be found)"
# display the lattice basis
if debug:
matrix_overview(BB, modulus^mm)
# LLL
if debug:
print "optimizing basis of the lattice via LLL, this can take a long time"
BB = BB.LLL()
if debug:
print "LLL is done!"
# transform vector i & j -> polynomials 1 & 2
if debug:
print "looking for independent vectors in the lattice"
found_polynomials = False
for pol1_idx in range(nn - 1):
for pol2_idx in range(pol1_idx + 1, nn):
# for i and j, create the two polynomials
PR.<w,z> = PolynomialRing(ZZ)
pol1 = pol2 = 0
for jj in range(nn):
pol1 += monomials[jj](w*z+1,w,z) * BB[pol1_idx, jj] / monomials[jj](UU,XX,YY)
pol2 += monomials[jj](w*z+1,w,z) * BB[pol2_idx, jj] / monomials[jj](UU,XX,YY)
# resultant
PR.<q> = PolynomialRing(ZZ)
rr = pol1.resultant(pol2)
# are these good polynomials?
if rr.is_zero() or rr.monomials() == [1]:
continue
else:
print "found them, using vectors", pol1_idx, "and", pol2_idx
found_polynomials = True
break
if found_polynomials:
break
if not found_polynomials:
print "no independant vectors could be found. This should very rarely happen..."
return 0, 0
rr = rr(q, q)
# solutions
soly = rr.roots()
if len(soly) == 0:
print "Your prediction (delta) is too small"
return 0, 0
soly = soly[0][0]
ss = pol1(q, soly)
solx = ss.roots()[0][0]
#
return solx, soly
def example():
############################################
# How To Use This Script
##########################################
#
# The problem to solve (edit the following values)
#
# the modulus
N = 0xbadd260d14ea665b62e7d2e634f20a6382ac369cd44017305b69cf3a2694667ee651acded7085e0757d169b090f29f3f86fec255746674ffa8a6a3e1c9e1861003eb39f82cf74d84cc18e345f60865f998b33fc182a1a4ffa71f5ae48a1b5cb4c5f154b0997dc9b001e441815ce59c6c825f064fdca678858758dc2cebbc4d27
# the public exponent
e = 0x11722b54dd6f3ad9ce81da6f6ecb0acaf2cbc3885841d08b32abc0672d1a7293f9856db8f9407dc05f6f373a2d9246752a7cc7b1b6923f1827adfaeefc811e6e5989cce9f00897cfc1fc57987cce4862b5343bc8e91ddf2bd9e23aea9316a69f28f407cfe324d546a7dde13eb0bd052f694aefe8ec0f5298800277dbab4a33bb
# the hypothesis on the private exponent (the theoretical maximum is 0.292)
#delta = .18 # this means that d < N^delta
delta = .18
#
# Lattice (tweak those values)
#
# you should tweak this (after a first run), (e.g. increment it until a solution is found)
m = 4 # size of the lattice (bigger the better/slower)
# you need to be a lattice master to tweak these
t = int((1-2*delta) * m) # optimization from Herrmann and May
X = 2*floor(N^delta) # this _might_ be too much
Y = floor(N^(1/2)) # correct if p, q are ~ same size
#
# Don't touch anything below
#
# Problem put in equation
P.<x,y> = PolynomialRing(ZZ)
A = int((N+1)/2)
pol = 1 + x * (A + y)
#
# Find the solutions!
#
# Checking bounds
if debug:
print "=== checking values ==="
print "* delta:", delta
print "* delta < 0.292", delta < 0.292
print "* size of e:", int(log(e)/log(2))
print "* size of N:", int(log(N)/log(2))
print "* m:", m, ", t:", t
# boneh_durfee
if debug:
print "=== running algorithm ==="
start_time = time.time()
solx, soly = boneh_durfee(pol, e, m, t, X, Y)
# found a solution?
if solx > 0:
print "=== solution found ==="
if False:
print "x:", solx
print "y:", soly
d = int(pol(solx, soly) / e)
print "private key found:", d
else:
print "=== no solution was found ==="
if debug:
print("=== %s seconds ===" % (time.time() - start_time))
if __name__ == "__main__":
example()7、[鹤城杯 2021]BabyRSA(已知p的高位和q的低位)
题目
from Crypto.Util.number import getPrime, bytes_to_long
from secret import flag
p = getPrime(1024)
q = getPrime(1024)
n = p * q
e = 65537
hint1 = p >> 724 #p的高位 300
hint2 = q % (2 ** 265) #q的低位 759
ct = pow(bytes_to_long(flag), e, n)
print(hint1)
print(hint2)
print(n)
print(ct)sage脚本
先求p的低位p0
mod=pow(2,265)
p0=n*gmpy2.invert(hint2,mod)%mod
print(p0)
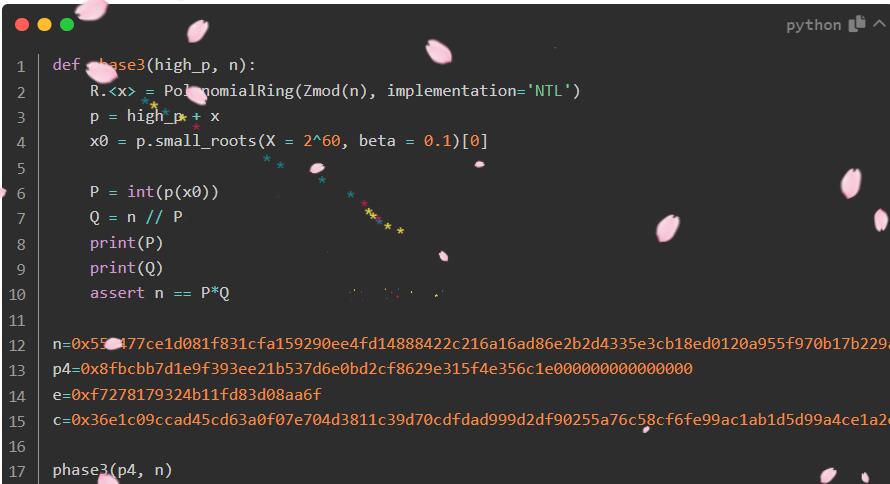
#30417487794073877577997977068358253483488121930635899911316665665825597484019031然后用sage脚本求p
p1 = 1514296530850131082973956029074258536069144071110652176122006763622293335057110441067910479
q0 = 40812438243894343296354573724131194431453023461572200856406939246297219541329623
n = 21815431662065695412834116602474344081782093119269423403335882867255834302242945742413692949886248581138784199165404321893594820375775454774521554409598568793217997859258282700084148322905405227238617443766062207618899209593375881728671746850745598576485323702483634599597393910908142659231071532803602701147251570567032402848145462183405098097523810358199597631612616833723150146418889589492395974359466777040500971885443881359700735149623177757865032984744576285054725506299888069904106805731600019058631951255795316571242969336763938805465676269140733371287244624066632153110685509892188900004952700111937292221969
mod=pow(2,265)
p0=30417487794073877577997977068358253483488121930635899911316665665825597484019031
pbar=(p1<<724)+p0
#sage
PR.<x> = PolynomialRing(Zmod(n))
for i in range(32):
f=pbar+x*mod*32
f=f.monic()
pp=f.small_roots(X=2^454,beta=0.4)
if(pp):
break
pbar+=mod
p=pbar+pp[0]*32*mod
assert n%p==0
print(p)然后利用利用脚本求flag
import gmpy2
import libnum
e = 65537
n = 21815431662065695412834116602474344081782093119269423403335882867255834302242945742413692949886248581138784199165404321893594820375775454774521554409598568793217997859258282700084148322905405227238617443766062207618899209593375881728671746850745598576485323702483634599597393910908142659231071532803602701147251570567032402848145462183405098097523810358199597631612616833723150146418889589492395974359466777040500971885443881359700735149623177757865032984744576285054725506299888069904106805731600019058631951255795316571242969336763938805465676269140733371287244624066632153110685509892188900004952700111937292221969
ct = 19073695285772829730103928222962723784199491145730661021332365516942301513989932980896145664842527253998170902799883262567366661277268801440634319694884564820420852947935710798269700777126717746701065483129644585829522353341718916661536894041337878440111845645200627940640539279744348235772441988748977191513786620459922039153862250137904894008551515928486867493608757307981955335488977402307933930592035163126858060189156114410872337004784951228340994743202032248681976932591575016798640429231399974090325134545852080425047146251781339862753527319093938929691759486362536986249207187765947926921267520150073408188188
p=133637329398256221348922087205912367118213472434713498908220867690672019569057789598459580146410501473689139466275052698529257254973211963162087316149628000798221014338373126500646873612341158676084318494058522014519669302359038980726479317742766438142835169562422371156257894374341629012755597863752154328407
q=n//p
phi=(p-1)*(q-1)
d = gmpy2.invert(e,phi)
m = pow(ct,d,n)
print(libnum.n2s(int(m)))
#flag{ef5e1582-8116-4f61-b458-f793dc03f2ff}