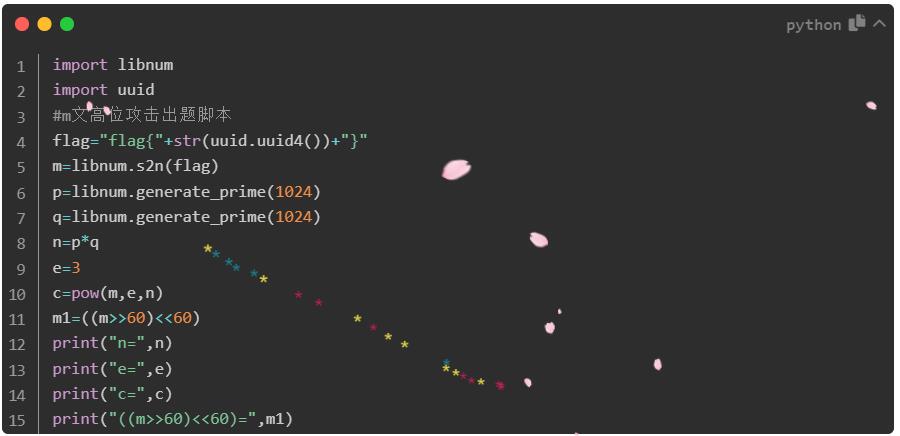
脚本1
根据题目,注意 2^60 60需要修改相应的位数 a = (p >> 60) << 60
def phase3(high_p, n):
R.<x> = PolynomialRing(Zmod(n), implementation='NTL')
p = high_p + x
x0 = p.small_roots(X = 2^60, beta = 0.1)[0]
P = int(p(x0))
Q = n // P
print(P)
print(Q)
assert n == P*Q
n=0x558477ce1d081f831cfa159290ee4fd14888422c216a16ad86e2b2d4335e3cb18ed0120a955f970b17b229a8e7d0ae1b6f0c40213ad0e127eba99ae0d8a82397
p4=0x8fbcbb7d1e9f393ee21b537d6e0bd2cf8629e315f4e356c1e000000000000000
e=0xf7278179324b11fd83d08aa6f
c=0x36e1c09ccad45cd63a0f07e704d3811c39d70cdfdad999d2df90255a76c58cf6fe99ac1ab1d5d99a4ce1a2ebdbfbc49ce72df2a0b90766ff84ab0ef62068d46b
phase3(p4, n) 脚本2
n = 22127806011633861727954101002390179580447625543207045612671617864341845851658260004006826435219665722338399712799144283442305160095371386129132285556214330279867129279885732638085139970894386809975772641941102438472230541606849251235636928502018782288977994793382547376630461074356449893196487276906629063423071245785206275636191377977712166746567658967286739276282635616277590864547265366547379387583014365390660407286148179073747800137068237371705680826025177248889969809158386539617738762070772471531610084135064141878988874470291949704156926711239213996266350299670204058121040684469621186909795304289942430452869
p4=0xd8bf1376aaae63b3c4d693ca7f3d8a76270b7310bb8bd4608a98c9fdd85fc1ccc7c246b364e2779034057f0ec7a101bad64269d9dcca69f9b5c3462b058b94db0987aa09426c5e7634b3e19f56872693206790c6feef0c9ae662d73f1b12c3cd
e = 0x10001
pbits = 1024
kbits = pbits - p4.nbits()
print(p4.nbits())
p4 = p4 << kbits
PR.<x> = PolynomialRing(Zmod(n))
f = x + p4
roots = f.small_roots(X=2^kbits, beta=0.4)
if roots:
p = p4+int(roots[0])
print ("n: ", n)
print ("p: ", p)
print ("q: ", n/p)