e和phi_n不互素

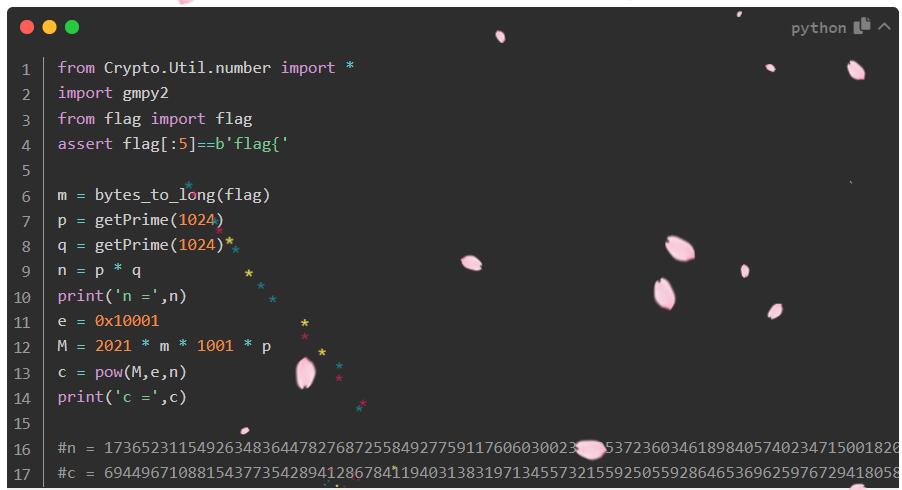
e和phi_n不互素是指它俩的公约数不为1

令t = gmpy2.gcd(e,phi)

1.m**t < n

出题脚本

import gmpy2
import libnum
import random
import uuid
flag="flag{"+str(uuid.uuid4())+"}"
m=libnum.s2n(flag)

while 1:
    e = random.randint(100,1000)
    p=libnum.generate_prime(1024)
    q=libnum.generate_prime(1024)
    phi_n=(p-1)*(q-1)
    t=gmpy2.gcd(e,phi_n)
    if  gmpy2.invert(e // t, phi_n) and t !=1:
        break
n=p*q
c=pow(m,e,n)
print("p=",p)
print("q=",q)
print("e=",e)
print("c=",c) 

解题脚本

import gmpy2
from Crypto.Util.number import *


# 当e约去公约数后与phi互素
def decrypt(p, q, e, c):
    n = p * q
    phi = (p - 1) * (q - 1)
    t = gmpy2.gcd(e, phi)
    d = gmpy2.invert(e // t, phi)
    m = pow(c, d, n)
    print(m)
    msg = gmpy2.iroot(m, t)
    print(msg)
    if msg[1]:
        print(long_to_bytes(msg[0]))

p= 127577058764408216374028752283743628765651360507566484643526093715329608267323381565274095814069864692746147152580906850350743742856555229701448239882612922698102985146366639955081466129923966803267071097174222576416224094182123529282235807472362341680183683025490897702891081336913842652559163341223338641607
q= 156492273708587234539506501480609692085997989594717058472605523051244522493701609615085173280972894139427194976925940854142835807192417391269823151398439665817176522629246535810290194301862945052149450578938260979300632842291287807430486629994530805358742405299538986591596966945727494262182814875780600646003
e= 750
c= 7029383721249299532521086933490698266831518266762255492452526410777276825803657150303837084263410309063739203644435184397762022380085273363900423091223180151147964276354189658062571415744140073426572149093499560918765793389358300893454490774387180728097370701432534877005948330689495694820361726719418371072834639369078180094444137972424909816959445043108154884587947573054460257114169961823509538355580857411319157089278918107229480661280354242839678709689654304688727345294473487201644985815128413154870914132135222144633969959773621933444285994038028721862094040876152694240238708737727034258171506516394913692187

decrypt(p, q, e, c) 

2、m**t > n

类型一.如果m**t没有比n大多少，那就可以爆破

from gmpy2 import iroot
p = 
q = 
c = 
n = p*q
e = 
k = 0
while not iroot(_m + k*n, t)[1]:
	k += 1
m = iroot(_m + k*n, t)[0]

其实就相当于转换成了一个低加密指数的题

类型2.也可以选择结合中国剩余定理

• $ x^e\equiv c\pmod{p} \ x^e\equiv c\pmod{q} $

from Crypto.Util.number import *
import gmpy2
'''
p = 
q = 
c = 
n = 
e = 
phi = (p - 1) * (q - 1)
'''
R.<x> = Zmod(p)[]
f = x ^ e - c
f = f.monic()
res1 = f.roots()

R.<x> = Zmod(q)[]
f = x ^e - c
f = f.monic()
res2 = f.roots()
for i in res1:
    for j in res2:
        ai = [i[0],j[0]]
        mi = [p,q]
        flag = CRT_list(ai,mi)
        flag = long_to_bytes(flag)
        if b'flag' in flag:
            print(flag)

例题 [强网杯 2022]ASR

from Crypto.Util.number import getPrime
from secret import falg
pad = lambda s:s + bytes([(len(s)-1)%16+1]*((len(s)-1)%16+1))

n = getPrime(128)**2 * getPrime(128)**2 * getPrime(128)**2 * getPrime(128)**2
e = 3
flag = pad(flag)
print(flag)
assert(len(flag) >= 48)
m = int.from_bytes(flag,'big')
c = pow(m,e,n)
print(f'n = {n}')
print(f'e = {e}')
print(f'c = {c}')
n = 8250871280281573979365095715711359115372504458973444367083195431861307534563246537364248104106494598081988216584432003199198805753721448450911308558041115465900179230798939615583517756265557814710419157462721793864532239042758808298575522666358352726060578194045804198551989679722201244547561044646931280001
e = 3
c = 945272793717722090962030960824180726576357481511799904903841312265308706852971155205003971821843069272938250385935597609059700446530436381124650731751982419593070224310399320617914955227288662661442416421725698368791013785074809691867988444306279231013360024747585261790352627234450209996422862329513284149

分解n得到
p = 225933944608558304529179430753170813347
q = 260594583349478633632570848336184053653
r = 218566259296037866647273372633238739089
t = 223213222467584072959434495118689164399
正常情况下的RSA都要求e和phi(n)要互素，不过也有一些e和phi(n)有很小的公约数的题目，这些题目可以通过计算e对phi(n)的逆元d来求解。但是本题则为e和phi(n)的最大公约数就是e本身，也就是说e | p-1，只有对c开e次方根才行,到这里就是一个有限域开3次方根的问题了。

$ m^e\equiv c\pmod{p} \ m^e\equiv c\pmod{q} \ m^e\equiv c\pmod{r} \m^e\equiv c\pmod{s}$

然后分别在GF（p）、GF(q)、GF（r）、GF(t)上对c开e=3次方根，再用CRT组合一下即可得到在mod n下的解

sage脚本

import libnum
n = 8250871280281573979365095715711359115372504458973444367083195431861307534563246537364248104106494598081988216584432003199198805753721448450911308558041115465900179230798939615583517756265557814710419157462721793864532239042758808298575522666358352726060578194045804198551989679722201244547561044646931280001
e = 3
c = 945272793717722090962030960824180726576357481511799904903841312265308706852971155205003971821843069272938250385935597609059700446530436381124650731751982419593070224310399320617914955227288662661442416421725698368791013785074809691867988444306279231013360024747585261790352627234450209996422862329513284149
p = 225933944608558304529179430753170813347
q = 260594583349478633632570848336184053653
r = 218566259296037866647273372633238739089
t = 223213222467584072959434495118689164399

R.<x> = Zmod(p)[]
f = x^e-c
f = f.monic()
results1 = f.roots()

R.<x> = Zmod(q)[]
f = x^e-c
f = f.monic()
results2 = f.roots()

R.<x> = Zmod(r)[]
f = x^e-c
f = f.monic()
results3 = f.roots()

R.<x> = Zmod(t)[]
f = x^e-c
f = f.monic()
results4 = f.roots()
for i in results1:
    for j in results2:
        for l in results3:
            for k in results4:
                param1 = [int(i[0]),int(j[0]),int(l[0]),int(k[0])]
                param2 = [p,q,r,t]
                m = CRT_list(param1,param2)
                flag = libnum.n2s(int(m))
                if b'flag'  in flag:
                    print(flag)
         
#b'flag{Fear_can_hold_you_prisoner_Hope_can_set_you_free}\x06\x06\x06\x06\x06\x06'

AMM有限域开方

例题 [NCTF 2019]easyRSA

题目

from flag import flag

e = 0x1337
p = 199138677823743837339927520157607820029746574557746549094921488292877226509198315016018919385259781238148402833316033634968163276198999279327827901879426429664674358844084491830543271625147280950273934405879341438429171453002453838897458102128836690385604150324972907981960626767679153125735677417397078196059
q = 112213695905472142415221444515326532320352429478341683352811183503269676555434601229013679319423878238944956830244386653674413411658696751173844443394608246716053086226910581400528167848306119179879115809778793093611381764939789057524575349501163689452810148280625226541609383166347879832134495444706697124741
n = p * q

assert(flag.startswith('NCTF'))
m = int.from_bytes(flag.encode(), 'big')
assert(m.bit_length() > 1337)

c = pow(m, e, n)
print(c)
10562302690541901187975815594605242014385201583329309191736952454310803387032252007244962585846519762051885640856082157060593829013572592812958261432327975138581784360302599265408134332094134880789013207382277849503344042487389850373487656200657856862096900860792273206447552132458430989534820256156021128891296387414689693952047302604774923411425863612316726417214819110981605912408620996068520823370069362751149060142640529571400977787330956486849449005402750224992048562898004309319577192693315658275912449198365737965570035264841782399978307388920681068646219895287752359564029778568376881425070363592696751183359

python脚本

from gmpy2 import *
from Crypto.Util.number import *
import random
import math

def onemod(e, q):
    p = random.randint(1, q-1)
    while(powmod(p, (q-1)//e, q) == 1):  # (r,s)=1
        p = random.randint(1, q)
    return p

def AMM_rth(o, r, q):  # r|(q-1
    assert((q-1) % r == 0)
    p = onemod(r, q)

    t = 0
    s = q-1
    while(s % r == 0):
        s = s//r
        t += 1
    k = 1
    while((s*k+1) % r != 0):
        k += 1
    alp = (s*k+1)//r

    a = powmod(p, r**(t-1)*s, q)
    b = powmod(o, r*a-1, q)
    c = powmod(p, s, q)
    h = 1

    for i in range(1, t-1):
        d = powmod(int(b), r**(t-1-i), q)
        if d == 1:
            j = 0
        else:
            j = (-math.log(d, a)) % r
        b = (b*(c**(r*j))) % q
        h = (h*c**j) % q
        c = (c*r) % q
    result = (powmod(o, alp, q)*h)
    return result

def ALL_Solution(m, q, rt, cq, e):
    mp = []
    for pr in rt:
        r = (pr*m) % q
        # assert(pow(r, e, q) == cq)
        mp.append(r)
    return mp


def calc(mp, mq, e, p, q):
    i = 1
    j = 1
    t1 = invert(q, p)
    t2 = invert(p, q)
    for mp1 in mp:
        for mq1 in mq:
            j += 1
            if j % 1000000 == 0:
                print(j)
            ans = (mp1*t1*q+mq1*t2*p) % (p*q)
            if check(ans):
                return
    return


def check(m):
    try:
        a = long_to_bytes(m).decode('utf-8')
        if 'NCTF' in a:
            print(a)
            return True
        else:
            return False
    except:
        return False


def ALL_ROOT2(r, q):  # use function set() and .add() ensure that the generated elements are not repeated
    li = set()
    while(len(li) < r):
        p = powmod(random.randint(1, q-1), (q-1)//r, q)
        li.add(p)
    return li


if __name__ == '__main__':
    c = 10562302690541901187975815594605242014385201583329309191736952454310803387032252007244962585846519762051885640856082157060593829013572592812958261432327975138581784360302599265408134332094134880789013207382277849503344042487389850373487656200657856862096900860792273206447552132458430989534820256156021128891296387414689693952047302604774923411425863612316726417214819110981605912408620996068520823370069362751149060142640529571400977787330956486849449005402750224992048562898004309319577192693315658275912449198365737965570035264841782399978307388920681068646219895287752359564029778568376881425070363592696751183359
    p = 199138677823743837339927520157607820029746574557746549094921488292877226509198315016018919385259781238148402833316033634968163276198999279327827901879426429664674358844084491830543271625147280950273934405879341438429171453002453838897458102128836690385604150324972907981960626767679153125735677417397078196059
    q = 112213695905472142415221444515326532320352429478341683352811183503269676555434601229013679319423878238944956830244386653674413411658696751173844443394608246716053086226910581400528167848306119179879115809778793093611381764939789057524575349501163689452810148280625226541609383166347879832134495444706697124741
    e = 0x1337
    cp = c % p
    cq = c % q

    mp = AMM_rth(cp, e, p)
    mq = AMM_rth(cq, e, q)

    rt1 = ALL_ROOT2(e, p)
    rt2 = ALL_ROOT2(e, q)

    amp = ALL_Solution(mp, p, rt1, cp, e)
    amq = ALL_Solution(mq, q, rt2, cq, e)

    calc(amp, amq, e, p, q)
#NCTF{T4k31ng_Ox1337_r00t_1s_n0t_th4t_34sy}