dp泄露

dp泄露

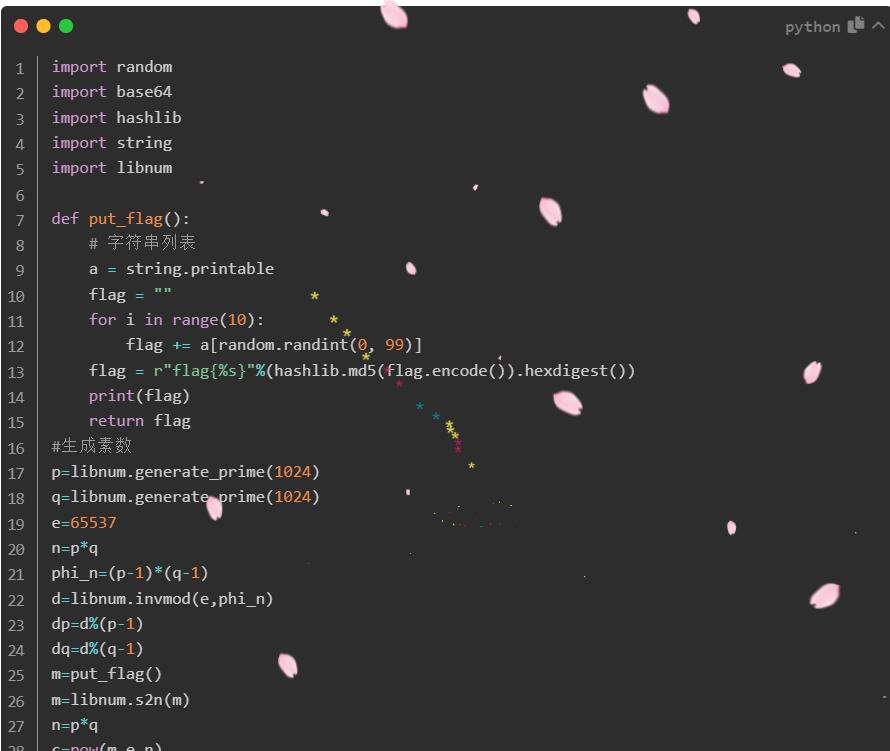
出题脚本

import random
import base64
import hashlib
import string
import libnum

def put_flag():
    # 字符串列表
    a = string.printable
    flag = ""
    for i in range(10):
        flag += a[random.randint(0, 99)]
    flag = r"flag{%s}"%(hashlib.md5(flag.encode()).hexdigest())
    print(flag)
    return flag

#生成素数
p=libnum.generate_prime(1024)
q=libnum.generate_prime(1024)
e=65537
n=p*q
phi_n=(p-1)*(q-1)
d=libnum.invmod(e,phi_n)
dp=d%(p-1)
m=put_flag()
m=libnum.s2n(m)
n=p*q
c=pow(m,e,n)

print("n=",n)
print("e=",e)
print("dp=",dp)
print("c=",c)

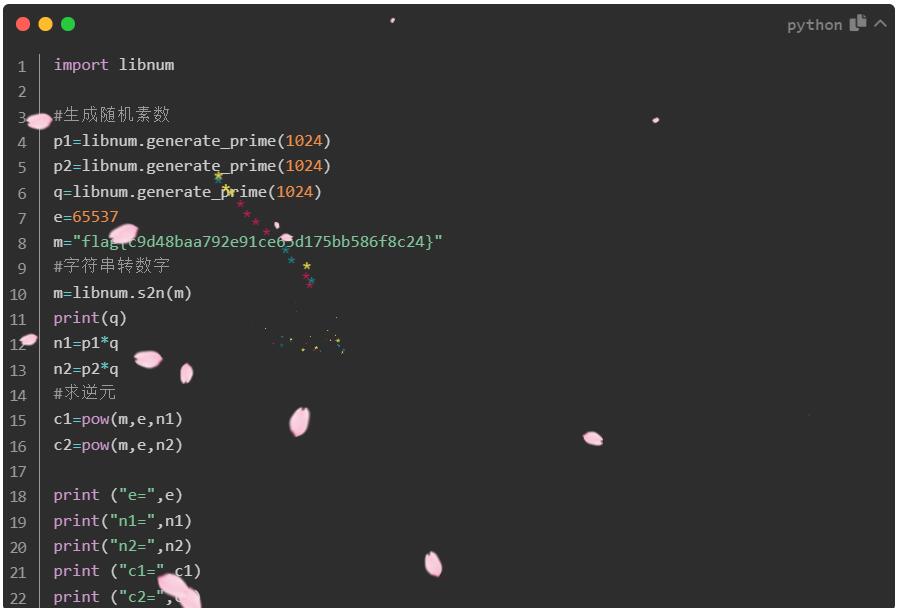
解密脚本

import libnum
import gmpy2

n= 15490329974794812647207350945845678224681604428642220566423366180973839697096441619340018253695472604335938643849069014103520861300713053955205392905536446156153192076633656788424185734898016745641378430506574498111680248029123341493733599302123100131134215957579162168779228208387783035893621162016993340603475960735061572761512755519616410410615413820180757126318567325096339342686253738778178380191340135516056457473854126752188188261914055391966730674861017432904735293451031131827880629989269835970170038295168392442835892108945315382078025510997711116410638765048886317360842562784200384045644008789130370444983
e= 65537
dp= 92421914522602787051376990773545034723755500322946639408033747477366773088952064561196722681757327451210117825346237003629597066505402384880737033044776720946764227004188812078355462119361676746112866393394866072449432108301690846327127554699521545673830710939287951837844749172755258073462248214264511338895
c= 11917967705200196530423914441613144297148147672566202863977167024519218321836386637302409557947445841293888462405994683655441879000427977086221906497225533946193332303182079068462781262341197088906792898634398410298474823088739257515556595214077227746604247505450334512424047100626106474291190033258919062850451435841454816600402372026810570127115167968899329724894556092798669018218440148846597174016217159034241427361756697433952800424383010684502324285145303400856470193420837017178412747680690628590204528459258189973779463979907863227915782407651254796209362605706066438960631045833533860845111845422613428738602

for i in range(1,65535):
    p=(dp*e-1)//i+1
    if n%p==0:
        q=n//p
        break
print(p)
print(q)
phi_n= (p-1)*(q-1)
d=gmpy2.invert(e,phi_n)
m=pow(c,d,n)
print(m)
flag=libnum.n2s(int(m)).decode()
print(flag)

题目解析

已知：

c = m^e mod n
m = c^d mod n
ϕ(n)=(p−1)*(q−1)
d∗e ≡ 1 mod ϕ(n)
dp = d mod (p−1)
由上式可以得到

dp*e≡d*e mod (p−1)
因此可以得到

式1：d∗e=k∗(p−1)+dp∗e
式2：d∗e≡1 mod ϕ(n)
式1带入式2

=> k∗(p−1)+dp∗e ≡1 mod ϕ(n)

=> k∗(p−1)+dp∗e ≡1 mod (p−1)∗(q−1)

=> k1∗(p−1)+dp∗e = k2*(p−1)∗(q−1)+1

=> dp*e =  k2*(p−1)∗(q−1)+1-k1∗(p−1)+dp∗e

=> dp*e = (p-1)*[k2*(p-1)-k1]+1
因dp<p−1（dp是d//（p-1）的余数，dp<p−1）

所以e > k2∗(q−1)−k1

假设 x=k2∗(q−1)−k1

x的范围为 (0,e)

x∗(p−1)+1=dp∗e

求出p-1方法，遍历(0,e)的范围，其中肯定有一个p可以被n整除，那么求出p和q