N不互素

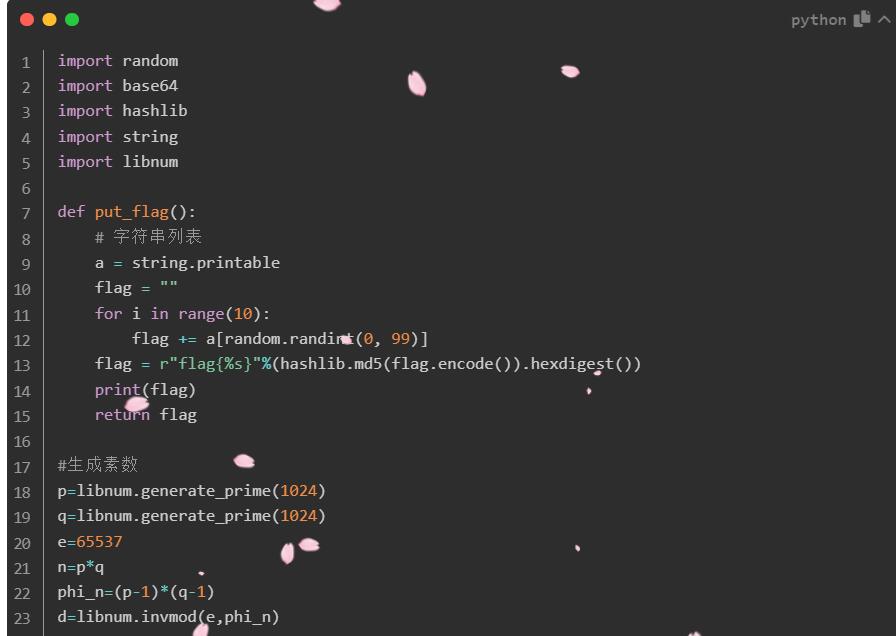
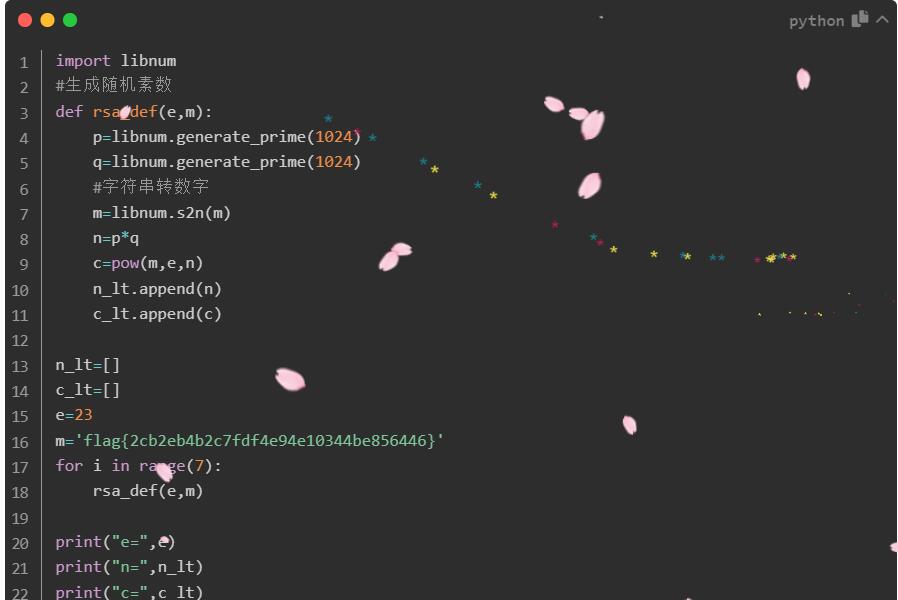
出题脚本1：

import libnum

#生成随机素数
p1=libnum.generate_prime(1024)
p2=libnum.generate_prime(1024)
q=libnum.generate_prime(1024)
e=65537
m="flag{c9d48baa792e91ce65d175bb586f8c24}"
#字符串转数字
m=libnum.s2n(m)
print(q)
n1=p1*q
n2=p2*q
#求逆元
c1=pow(m,e,n1)
c2=pow(m,e,n2)

print ("e=",e)
print("n1=",n1)
print("n2=",n2)
print ("c1=",c1)
print ("c2=",c2)

解题脚本：

import libnum
import gmpy2

e= 65537
n1= 18851781425565649500243914718895527060598553785142033499277947796047289729069551538151421839511239897691881228121437622923274745439286192958624933347473814433650645821240330239352230328910532686189064529002598986350545013596873280380093139589440286483854335646063005690269032198568724965964443111093291700142910652223408636268615176273268372177721667944316123253596652992256076572634227395015036348109972259736684061785035583511127926569341967394058493301139935304361924639075754092181040235419401702148068770694697982444290753353433701503833775179671108406498799549700127209151389161427718168658930877516526900193773
n2= 24141384186719901100738328229558939321137195844627407412035205930880546126459260897433418685279927024995699136588216700770429628894224051287181657357533218989737870319139269421990248988961435374202640406264110282763206906390508271179764960952342404379846442988489435158217691170804372863828966379599925114485971708200189788312061335938149982724447336254731731196164294152411281627551943972751739099703406466680639123738668207648503911709799873188331259979032169198913999856215096219340617703116234922400948884716827963616800355410477122406692338452507358998811789750057925245184372948089354754021196407808558611706347
c1= 11233930138929485738604185458820792679941706517184575056860307907280050814616639358486313129298273947905894904145194035804995663173314907762677924041275132974029028894644172713486633713023630611556983846927634063704894533048653309657581762974450289360550659261899944333557732087882069544235529266455787027619668939220511057340231613645208599303911724024926701608537602920797245075262273603379467945283128416767718651714209330369788240996832207630345743245279821753430782200336283582459635492184924556145031704499178500242816865275291936063430100028447772122941596704727728675661250380470986371668037469383671505328135
c2= 5585224206647236865248808202221713289466135149339680308821203835812670001259895780508640505222648200259525489427033258746992319005320440650548405653844536422632581252608192223771882550003217335273112474383014796651892287737753603533030776710121680439078567046997872719450037145665867123925472406058893384600128119493338790196284996386511009366274826447064392594100457497289556291407982935292829015102796178711091471748295065093460144885719356062242014650190112796869173536886083200906303200902844575328314123662659807283984619970501020349836850699532193026247740142876327310689901499496665093919484517214474842110431


#求最大公约数
q=gmpy2.gcd(n1,n2)
p1=n1//q

phi_n=(q-1)*(p1-1)
#求逆元d
d1=libnum.invmod(e,phi_n)
m=pow(c1,d1,n1)
print(m)
#数字转字节，转字符串
print(libnum.n2s(int(m)).decode())