共模攻击

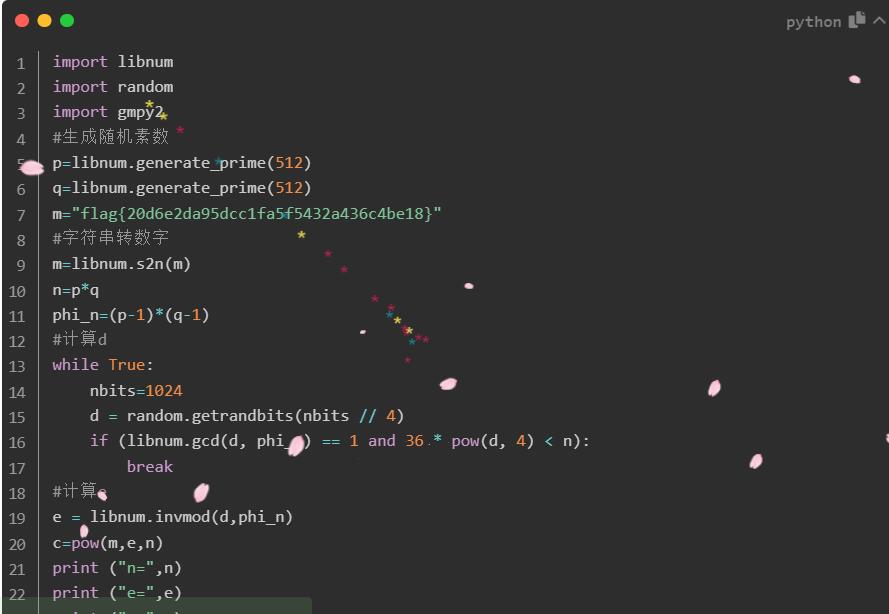
共模攻击，利用的大前提就是，RSA体系在生成密钥的过程中使用了相同的模数n。在CTF题目中，就是同一明文，同一n,不同e进行加密。m,n相同；e,c不同，且e1和e2互质

出题脚本：

import libnum
import gmpy2
#生成素数
p=libnum.generate_prime(1024)
q=libnum.generate_prime(1024)
e1=2333
e2=23333
m="flag{6ed4c74e022cb18c8039e96de93aa9ce}"
m=libnum.s2n(m)
n=p*q
c1=pow(m,e1,n)
c2=pow(m,e2,n)
print("n1=",n)
print("e1=",e1)
print("c1=",c1)
print("n2=",n)
print("e2=",e2)
print("c2=",c2)

解密脚本：

import gmpy2
import libnum

n= 25333966058003377512707481338795714713737652659944601834182685873529702913988641983855700459996104700470621411559153944988952210084014634675583566338568882440708528997808798650962116756969822211586531522430245040013570571043385238601846104615050089457836721437790715225367971106085839523500735480715155424498941150468093083816830215632716244390679417218873179734276657411907216486790815037105108306055794473002315541787461904728375164737225486501009857299717749346279371251245318729951905832578739696926931502225899707226264570557623527701806829827566904224572897378639191756878049342203546309520458672464170859577433
e1= 2333
c1= 11355981897781478907853356911752561659125575027336719997290835661089901154031171698660586203170528368228850895159361637188990782030255983633790580700032092629587631108597144196551438410868034739981960656110887650747325311613900008001234835897835613759692146419080113176963747835592656185435741504176116672174539018089139547795447109458469225330809064539216773123671814859510069089532677704482026169178543062578686794346026774853085101278125763460212801929360456888869350105294595904940799522522144740464043605342348269086324747729288399275079874271519208155039364092577755518532799345651172433227745483422620900776136
e2= 23333
c2= 1326499538902841116411674554069945581390130048432351353260154261863309471312810811160302458644816390944833633923435634961251092531893503039914793217247984595331920909367627316087404934402312358642315675486438968585084964845763881078835787872160374025547400141298650794551970291119975344578667689961134814676553190178139842507675899262024572370313939107080072875068218336255452161407859907308656094331557912187788276334833723893856310434523337557011032081467262457427167978528280339494077785813461280853735266463152709443731638714219391773144349752633555310299318290576258086971373777118482642702020599928071855133041

#共模攻击
#共模攻击函数
def rsa_gong_N_def(e1,e2,c1,c2,n):
    e1, e2, c1, c2, n=int(e1),int(e2),int(c1),int(c2),int(n)
    s = gmpy2.gcdext(e1, e2)
    s1 = s[1]
    s2 = s[2]
    if s1 < 0:
        s1 = - s1
        c1 = gmpy2.invert(c1, n)
    elif s2 < 0:
        s2 = - s2
        c2 = gmpy2.invert(c2, n)
    m = (pow(c1,s1,n) * pow(c2 ,s2 ,n)) % n
    return int(m)
m = rsa_gong_N_def(e1,e2,c1,c2,n)
print(m)
print(libnum.n2s(int(m)))

共模攻击原理：

两个及以上的公钥(n,e)来加密同一条信息m

c1 = pow(m, e1, n)
c2 = pow(m, e2, n)

e1，e2互质，则有

gcd(e1,e2)=1

根据扩展欧几里德算法 对于不完全为 0 的整数 a，b，gcd（a，b）表示 a，b 的最大公约数。那么一定存在整数 x，y 使得 gcd（a，b）=ax+by

e1*s1+e2*s2 = 1

s1、s2皆为整数，但是一正一负，假设s1为正数,s2为负数

因为

c1 = m^e1%n
c2 = m^e2%n

可得：

(c1^s1*c2^s2)%n = ((m^e1%n)^s1(m^e2%n)^s2)%n

根据模运算性质： 幂运算是一种关于幂的数学运算。同底数幂相乘，底数不变，指数相加。同底数幂相除，底数不变，指数相减。幂的乘方，底数不变，指数相乘。

(a * b) % p = (a % p * b % p) % p
a ^ b % p = ((a % p) ^ b) % p

简化公式为：

(c1^s1*c2^s2)%n = ((m^e1%n)^s1*(m^e2%n)^s2)%n

=> (c1^s1*c2^s2)%n = ((m^e1%n)^s1%n*(m^e2%n)^s2%n)%n #(a * b) % p = (a % p * b % p) % p

=> (c1^s1*c2^s2)%n = ((m^e1)^s1%n*(m^e2)^s2%n)%n #((a % p) ^ b) % p =a ^ b % p

=> (c1^s1*c2^s2)%n = ((m^e1)^s1*(m^e2)^s2)%n # (a % p * b % p) % p=(a * b) % p

=>(c1^s1*c2^s2)%n = ((m^(e1*s1)*(m^(e2*s2))%n #。幂的乘方，底数不变，指数相乘。

(c1^s1*c2^s2)%n = (m^(e1*s1+e2*s2))%n  # 同底数幂相乘，底数不变，指数相加。

因为 e1s1+e2s2 = 1 得：

(c1^s1*c2^s2)%n = (m^1)%n

(c1^s1*c2^s2）%n=m

上述就是rsa共模攻击的过程

因此，同一m，同一n,不同e，进行加密。在不需要知道d的情况下，可以进行解密。